The Cosine Law by Similarity

The Law of Cosines establishes a relationship between the angles and the side lengths of \(\Delta ABC\):

\(c^{2} = a^{2} + b^{2} - 2ab\cdot \mbox{cos}\gamma,\)

where \(\gamma\) is the angle in \(\Delta ABC\) opposite side \(c\).

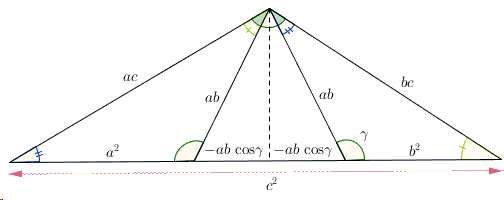
This proof without words submitted by Anders Kaseorg combines together \(3\) similar triangles; but where is the third? The proof was actually published at the American Mathematical Monthly, 121, February 2014, p 149, by Miles Dillon Edwards.

(There are several theorems that are proved by similar technique.)

• The Law of Cosines (Cosine Rule)
• The Illustrated Law of Cosines
• The Law of Sines and Cosines
• The Law of Cosines: Plane Tessellation
• The Law of Cosines: after Thâbit ibn Qurra
• The Law of Cosines: Unfolded Version
• The Law of Cosines (Independent of the Pythagorean Theorem)
• The Cosine Law by Similarity
• The Law of Cosines by Larry Hoehn
• The Law of Cosines - Another PWW
• The Law of Cosines - Yet Another PWW
• Law of Cosines by Ancient Sliding
• The Cosine Law: PWW by S. Kung

|Contact| |Front page| |Contents| |Geometry| |Up|

Copyright © 1996-2018 Alexander Bogomolny