Pythagoras' Theorem by Tessellation
This is a subtle and beautiful proof. It's quite easy to get an insight into why it works. The applet below is supposed to serve this purpose. The Pythagorean Theorem claims that 
are sides whereas c is the hypotenuse of a right-angled triangle. For the sake of the proof, we tasselate the plane into two grids. One is composed of the repeated pattern of two touching squares with sides a and b. The second grid consists of squares of side c parallel (and perpendicular) to the hypotenuse of the given triangle. These two grids have a common feature: they both are invariant under translation to the vector c parallel to the hypotenuse and of the same length. Note that this translation is equivalent to first translating the plane horizontally to the length of one side (say, a) and then vertically to the length of another (b). The insight might be gained when the two grids are superimposed as in the applet. Because of the above mentioned property the second grid cuts the first one into parts that may be combined in at least two different ways: to form two squares
The applet may be in two states. In the first you modify a right-angled triangle. In the second you drag the second grid to observe various "proofs" of the Pythagorean Theorem. All the operations are performed by dragging the mouse.
| What if applet does not run? |
Hubert Shutrick came up with a proof by dissection as depicted below:
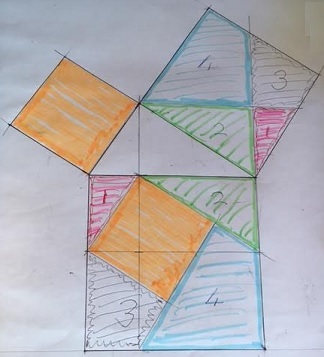
The above applet leads to a continuum multitude of proofs by dissection. Here's the one related to Hubert Shutrick's construction:
Reference
- K. O. Friedrichs, From Pythagoras to Einstein, MAA, 1965
|Contact| |Front page| |Contents| |Geometry| |Pythagorean Theorem|
Copyright © 1996-2018 Alexander Bogomolny71222967