Law of Cosines by Ancient Sliding

As is common, we shall denote the sides of $\Delta ABC$ opposite vertices $A,B,C$ as $a,b,c$ and the enclosed angles as $\alpha,\beta,\gamma.$

$c^{2}=a^{2}+b^{2}-2ab\cos\gamma.$

This simple and elegant proof mimics the sliding argument that was used, for example, in Proof 69 of the Pythagorean theorem but applies it to a modification of Proof 9. The foundation of the proof below lies on the equality of blue areas (where in the left part the blue figure is a square with side $c$):

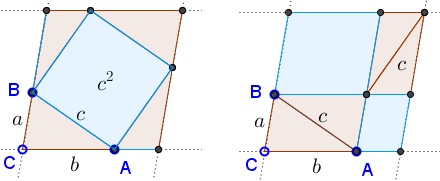
This is the same as the assertion in the Proof 55 of the Pythagorean theorem, though much more intuitive and straightforward.

The equality of the blue areas is sufficient to establish the Pythagorean theorem; for the Cosine Law we'll find explicit formulas for the areas of the parallelograms. The main tool here is an identity already used in another proof of the Law of Cosines:

(1)

$a=c\cos\beta+b\cos\gamma.$

The formula is explained in the following diagram:

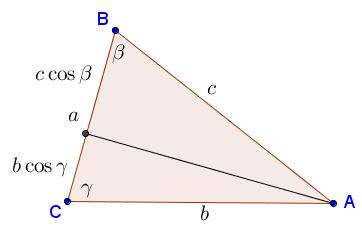
Note that the formula works also when either $\beta$ or $\gamma$ is obtuse. The next step is to identify the angles in the configuration:

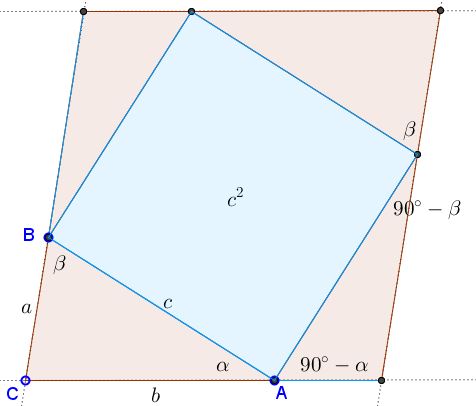
The next diagram now elucidates the expressions for the areas of small blue parallelograms.

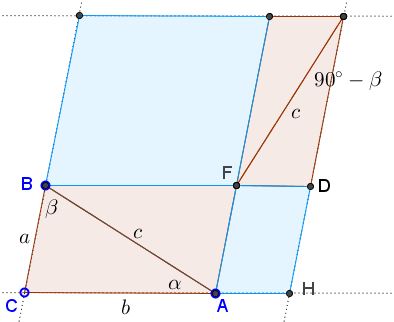
In the diagram, the distance from $F$ to $DH$ equals $c\sin(90^{\circ}-\beta)=c\cos\beta,$ which, along with (1), gives the distance as $h=a-b\cos\gamma$ so that the area of the lower parallelogram equals

$a\cdot h=a(a-b\cos\gamma )=a^{2}-ab\cos\gamma.$

Similarly, the area of the upper parallelogram equals $b^{2}-ab\cos\gamma$ which together add up to the Law of Cosines.

The proof has been posted by Mike Todd as a comment on another page devoted to the Law of Cosines.