The Law of Cosines: What is this about?
A Mathematical Droodle

---

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

---

What if applet does not run?

(The three vertices of triangle ABC are draggable as is the triangle itself.)

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

The applets suggests a proof of the Law of Cosines. The proof is a modification of the one communicated to me by Douglas Rogers. The latter is a direct generalization of Thâbit ibn Qurra's proof of the Pythagorean proposition. The latter has an unfolded version, which is generalized by the present proof.

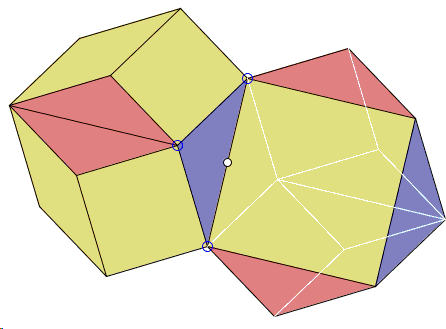
As in its relative, an important observation is that CP is equal and perpendicular to AB. Indeed, triangles ABC and CTR are friendly, which implies that the median of the latter through the vertex C is altitude of the former. But, since CTPR is a parallelogram, its diagonals divide each other into equal halves, CP is indeed the median of ΔCTR.

Also, the whole diagram appears to be symmetric in the midpoint O of AB.

• The Law of Cosines (Cosine Rule)
• The Illustrated Law of Cosines
• The Law of Sines and Cosines
• The Law of Cosines: Plane Tessellation
• The Law of Cosines: after Thâbit ibn Qurra
• The Law of Cosines: Unfolded Version
• The Law of Cosines (Independent of the Pythagorean Theorem)
• The Cosine Law by Similarity
• The Law of Cosines by Larry Hoehn
• The Law of Cosines - Another PWW
• The Law of Cosines - Yet Another PWW
• Law of Cosines by Ancient Sliding
• The Cosine Law: PWW by S. Kung

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny