A Neglected Pythagorean-Like Formula
A generalization of the Pythagorean Theorem has been published by Larry Hoehn (2000), whose article has been also included in C. Pritchard's collection.

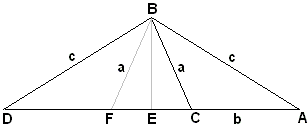
In an isosceles triangle with sides c draw a cevian of length a and assume its foot divides the base into segments b and d. Then [Hoehn]
| (1) | c2 = a2 + bd. |
The statement is a clear generalization of the Pythagorean theorem. The latter is obtained when the selected cevian coincides with the axis of symmetry (altitude, median, angle bisector) of the triangle, i.e. the case where
On the other hand, (1) can be derived by a double application of the Pythagorean theorem. Indeed, let the triangle be ABD, with the cevian BC. Draw the axis BE. From the right triangle ABE,
| (2) | c2 = BE2 + AE2. |
From the right triangle CBE,
| (3) | a2 = BE2 + EC2. |
Subtracting (3) from (2) we get
| (4) |
|
where (with FE = EC) AE + EC = AF = CD = d.
The proof reminds one of a proof of the law of cosines to which (1) appears to be related. Indeed,
d = CD = AF = AC + 2·EC,
so that (1) is the same as
| (5) | AB2 = BC2 + AC2 + 2·EC·AC, |
which is Euclid II.12 for ![]() ABC.
ABC.
On the other hand,
b = AC = DF = DC - 2·EC.
Thus (1) is the same as
| (6) | BD2 = BC2 + DC2 - 2·EC·DC, |
which is Euclid II.13 for ![]() BCD.
BCD.
This is a nice property: a single formula (1) covers both cases - for obtuse and acute angles - that Euclid treats separately. This is exactly a feature of the law of cosines, where the behavior of cosine absorbs the change of sign between (5) and (6).
Remark
Nathan Bowler observed that a simpler proof is obtained from the intersecting chords theorem applied in a circle with radius c centered at B. Extend BC in both directions to the intersection with the circle. Now you have two chords that meet at C:
(c - a)·(c + a) = bd.
Ricardo Sandoval adds to that that point C may lie outside segment AD in which case Power of a Point theorem leads to
(a - c)·(a + c) = bd,
or the same identity with one of b or d thought negative.
References
- T. L. Heath, EUCLID: The Thirteen Books of The Elements, books I and II, Dover, 1956
- L. Hoehn, A Neglected Pythagorean-Like Formula, Mathematical Gazette, 84 (2000), pp. 71-73
- C. Pritchard, The Changing Shape of Geomtetry, Cambridge University Press, 2003, pp. 228-231
Power of a Point wrt a Circle
- Power of a Point Theorem
- A Neglected Pythagorean-Like Formula
- Collinearity with the Orthocenter
- Circles On Cevians
- Collinearity via Concyclicity
- Altitudes and the Power of a Point
- Three Points Casey's Theorem
- Terquem's Theorem
- Intersecting Chords Theorem
- Intersecting Chords Theorem - a Visual Proof
- Intersecting Chords Theorem - Hubert Shutrick's PWW
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73569723
