The Cosine Law: PWW by S. Kung

This is a proof by Sidney H. Kung:

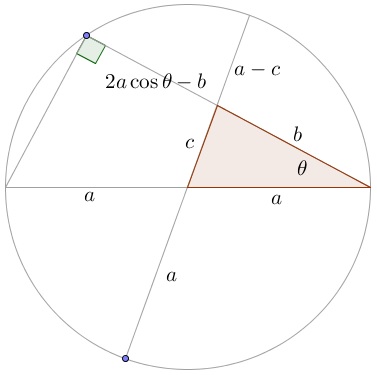
By the Intersecting Chords Theorem,

$(a+c)(a-c)=(2a\cos\theta-b)b,$

i.e., $a^2-c^2=2ab\cos\theta -b^2.$

References

1. R. B. Nelson, Proofs Without Words, MAA, 1993, p. 32

• The Law of Cosines (Cosine Rule)
• The Illustrated Law of Cosines
• The Law of Sines and Cosines
• The Law of Cosines: Plane Tessellation
• The Law of Cosines: after Thâbit ibn Qurra
• The Law of Cosines: Unfolded Version
• The Law of Cosines (Independent of the Pythagorean Theorem)
• The Cosine Law by Similarity
• The Law of Cosines by Larry Hoehn
• The Law of Cosines - Another PWW
• The Law of Cosines - Yet Another PWW
• Law of Cosines by Ancient Sliding
• The Cosine Law: PWW by S. Kung

|Contact| |Front page| |Contents| |Geometry| |Up|

Copyright © 1996-2018 Alexander Bogomolny