Angle Trisection by Paul Vjecsner
I have recently received a letter from Paul Vjecsner, a New York thinker and an amateur mathematician. Among several claims made, there was also a neusis angle trisection illustrated by an applet below. Paul mentions an impossibility result I am not aware of:
... the below angle trisection is achieved--applying Archimedian "neusis" or "sliding"--by unmarked ruler and compass, which is held impossible.
Other than that, the construction is almost on a par with a better known ones by, say, Archimedes, Hippocrates or by paper folding.
To quote from a Paul Vjecsner's letter:
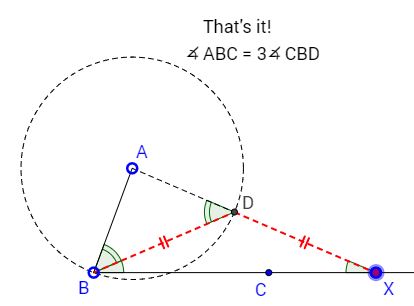
Briefly, given angle ABC, with a center D, to be on arc BD of random center A on that angle, draw arc BC such that A, D, and C are in a straight line. Angle DBC is then one third of angle ABC by Euclid's Proposition I.32.
(In all honesty I am not sure about the meaning of that instruction. The applet below reflects on my perception. X is a movebale point on BC. AX plays the role of the "ruler". The applet offers a shortcut to Paul's construction as I understand it.)
14 February 2016, Created with GeoGebra
The proof a simple: assume A, X, D are collinear.
Then triangles ABD and BDX are isosceles:
∠ABD = ∠ADB and
∠DBC = ∠DXB.
From the latter
∠BDX = 180° - 2∠DBX.
On the other hand, ∠BDX is exterior to ΔABD such that:
∠BDX = ∠ABD + ∠BAD = 180° - ∠BAD.
If we compare the two identities we'll see that
∠ABD = 2∠DBC,
or,
∠ABC = 3∠DBC.
However it is worth pondering which geometric tools have been actually used in the construction. How exactly does one achieve the collinearity of A, C and D? The process appears to be a loop repeating the following steps:
- Choose D on the circle centered at A and radius AB,
- Find the intersection of the circle centered at D and radius BD with the other (not containing A) leg of the given angle,
- Find the intersection of AD with that leg,
- Repeat 1-3 until two intersections coincide.
Paul quotes from his correspondence with Prof. Robin Hartshorne of the University of California, Berkeley who wondered whether the tool in Paul's proof was equivalent to the marked ruler. Paul did not have an answer to that question and I do not either.
|Activities| |Contact| |Front page| |Contents| |Geometry| |Eye opener|
Copyright © 1996-2018 Alexander Bogomolny
73579862
