Family Size
Problem 1
Consider a couple beginning a family; in the interest of promoting a diverse family, they decide to have children until they have both sexes. How many children can they expect to have?
Hint
We have already solved a very similar problem estimating the number of (Bernoulli) trials until the first success. The idea there was to evaluate probabilities of a sequence of trials having a certain length and then sum up an infinite series.
Solution of Problem 1
Assume $p$ is the probability of having a boy, $1-p$ that of having a girl. The sample space for our problem consists of just two kinds of sequences:
$BB\ldots BG$ and $GG\ldots GB.$
For a sequence of length $n,$ the probabilities are $(1-p^{n-1}p$ and $p^{n-1}(1-p),$ respectively, $n\ge 2.$ The mathematical expectation is then
$\begin{align}\displaystyle \sum_{n=2}^{\infty}&n((1-p^{n-1}p + p^{n-1}(1-p)) \\ &= p(1-p)\sum_{n=2}^{\infty}n((1-p)^{n-2}+p^{n-2}) \\ &= p(1-p)\bigg(\frac{2-p}{(1-p)^2}+\frac{2-(1-p)}{(1-(1-p))^2}\bigg) \\ &= \frac{1-p+p^2}{p(1-p)}. \end{align}$
(For a way to obtain such sums in a closed form see a separate discussion.)
This result sits well with the formula $E=\frac{1}{p}$ for the expected length of a sequence of trials until the first success. Since the series in the latter starts with with $p$ which is omitted as meaningless in the present problem, we would get
$\displaystyle\bigg(\frac{1}{p}-p\bigg)+\bigg(\frac{1}{1-p}-(1-p)\bigg)=\frac{1-p+p^2}{p(1-p)},$
conforming our calculations. The graph of $\displaystyle f(p)=\frac{1-p+p^2}{p(1-p)}$ shows that the expectation is at minimum when $p=1/2$ and goes to infinity as $p$ approaches either $0$ or $1.$
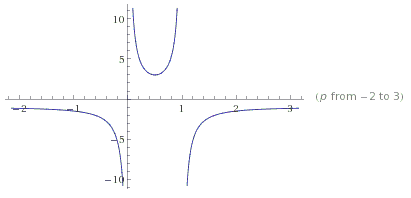
For $p=1/2,$ the expectation equals $3.$
Problem 2
Consider a couple beginning a family; At the outset they decide they will have children until they have a child of the same sex as the first one. How many children can they expect to have?
Solution of Problem 2
The sample space for this problem consists of sequences
$GBB\ldots BG$ and $BGG\ldots GB$
that, for length $n\ge 2,$ come with probabilities $(1-p)^{2}p^{n-2}$ and $p^{2}(1-p)^{n-2},$ respectively. The expectation then is given by
$\begin{align}\displaystyle E &= \sum_{n=2}^{\infty}n((1-p)^{2}p^{n-2}+p^{2}(1-p)^{n-2}) \\ &= \frac{(1-p)^2}{p^2}\sum_{n=0}^{\infty}np^{n}+\frac{p^2}{(1-p)^2}\sum_{n-2}^{\infty}n(1-p)^{n} \\ &= \frac{(1-p)^2}{p^2}S(p)+\frac{p^2}{(1-p)^2}S(1-p), \end{align}$
where $\displaystyle S(q)=\sum_{n=2}^{\infty}nq^n.$
I leave computing $\displaystyle S(q)=\frac{q^{2}(2-q)}{(1-q)^2}$ so that the expectation in this case is given by
$\displaystyle \begin{align} E &= \frac{(1-p)^2}{p^2}\frac{p^2(2-p)}{(1-p)^{2}}+\frac{p^2}{(1-p)^2}\frac{(1-p)^2(1+p)}{p^{2}}\\ &= (2-p) + (1+p) = 3. \end{align}$
Independent of $p\,!$ Which is a great surprise in its own right. But there is more. Note that the formula has been derived under an implicit assumption that $p$ is neither $0$ nor $1.$ But what if, say, $p=0?$ What if, by a fluke of fate, women stopped producing boys. Then obviously the only possible children component in a family would be two girls. In another extreme $(p=1)$, all families would consist of two boys. Although neither case is plausible, I think that the circumstance merits being mentioned as a naturally occurring discontinuity.
A diversion

Moscow street board promoting beds and sofas under the slogan "Foster increase of the nativity rate."
References
- P. Nahin, Duelling Idiots and Other Probability Puzzlers, Princeton University Press, 2000, pp 55-57
- What Is Probability?
- Intuitive Probability
- Probability Problems
- Sample Spaces and Random Variables
- Probabilities
- Conditional Probability
- Dependent and Independent Events
- Algebra of Random Variables
- Expectation
- Probability Generating Functions
- Probability of Two Integers Being Coprime
- Random Walks
- Probabilistic Method
- Probability Paradoxes
- Symmetry Principle in Probability
- Non-transitive Dice
![]()
|Contact| |Front page| |Contents| |Algebra| |Probability|
Copyright © 1996-2018 Alexander Bogomolny73579160
