 |
Cut The Knot!by Alex Bogomolny |
Parrondo Paradox
June 2001
|
... two ugly parents can have beautiful children ... Doron Zeilberger on receiving the 1998 Leroy P. Steele Prize |
Parrondo's Paradox is a double shocker. Counter to common intuition, it is possible to mix two losing games into a winning combination. This is a good news. But do not rub your hands just yet. The theory does not apply to casino games. Learning about it all must be its own reward. On the positive side but shaky ground, Sandra Blakeslee reported last year in NY Times that Dr. Sergei Maslov from Brookhaven National Laboratory had shown that if an investor simultaneously shared capital between two losing stock portfolios, capital would increase rather than decrease. (On the downside, as of the time of writing, it was too early to apply his model to the real stock market because of its complexity.)
Since the Paradox has been reported a couple of years ago, many real world and abstract examples has been thought up that make it more palatable. Indeed, monetary rewards apart, a combination of negative trends may lead to a positive outcome.
Brooke Buckley, an undergraduate student from Eastern Kentucky University, mentions in her honors thesis that it's a well known fact in agriculture, "that both sparrows and insects can eat all the crops. However, by having a combination of sparrows and insects, a healthy crop is harvested."(*)
In the above mentioned article, Sandra Blakeslee quotes Dr. Derek Abbott from Adelaide University who saw in public attitude towards the Monica Lewinsky affair a manifestation of a similar phenomenon. "President Clinton, who at first denied having a sexual affair with Monica S. Lewinsky saw his popularity rise when he admitted that he had lied. The added scandal created more good for Mr. Clinton."
As every one knows, Mr. Clinton was less lucky in his quest for the Nobel Prize, although, in 1993, he helped sponsor the Nobel Prize for Peace for Yassar Arafat - an archterrorist and a pathological liar. The paradox did work for the latter.
In an insightful paper by Shalosh B. Ekhad and Doron Zeilberger (both from Temple University), the authors make a point that the order of the intermingling activities may be of real importance. Although they mostly apply their theory to mundane situations, like walking, driving and flying, we may use their observation with the aforementioned cases. For example, lying publicly first (e.g., during the election campaigns) and then having an extramarital affair did not gain Mr. Clinton any points with the public.
The applet below emulates a well known battery-driven toy. A typical toy usually combines a stationary and a moving staircases; the latter moves periodically up and down. On the way up, the moving part picks a small something (a ball, a seal figurine) and deposits it on a stationary stair only to snatch it again a moment later and to deposit it on the next stair up. From the top of the stairs the piece slides to the bottom of the toy, from where the process starts over again. In the applet, I added some downward motion with the view of making the demonstration superficially more relevant to Parrondo's Paradox. (Presently, there's no applet. Sorry)
But what is Parrondo's Paradox? There are several writeups available on the Web including the original article by Derek Abbott and Greg Harmer in Nature magazine (vol. 402, 23/30 Dec 1999, p 864). The magazine charges an outrageous amount of $7 for a 1 page brief communication that is available any way (along with many other papers) at Greg's site (which has since been moved.) (Compare this with the attitude of A K Peters that made freely available the book
Of the two losing games -- A and B -- the first one is simple, the other one is complicated. In simple game A, one wins or loses $1 with probabilities p and 1-p, respectively. Game B is itself a combination of two games, say B1 and B2, both being as simple as game A. In game B1 probability of winning $1 is p1, in B2 it's p2. In B, game B1 is played if the current capital is a multiple of an integer
The catch here is that, in order for the paradox to occur, all three games A, B1, and B2 can't be losing. A typical assignment of probabilities would be
(As in the original paper by D. Abbott and G. Harmer, in the applet below, games A, B1, B2 are won with probabilities
Games A and B may be combined in many different ways. They can be combined randomly with a prescribed probability of selecting, say A. Or, their selection may follow a periodic pattern, like AABB, which means deterministicly playing two A games, followed by two B games, followed by two A's, and so on. The applet allows one to define up to 7 combinations (9 is the number of distinct colors that I clearly recognize as different in my browser. Games A and B take up two of the colors.) Just type the strings of A's and B's or real numbers (for probabilities) separated by space in the edit control at the bottom of the applet. Each trial consists of a specified number of games (100, originally), and you can also specify the number of trials (500, originally). (Presently, there's no applet. Sorry)
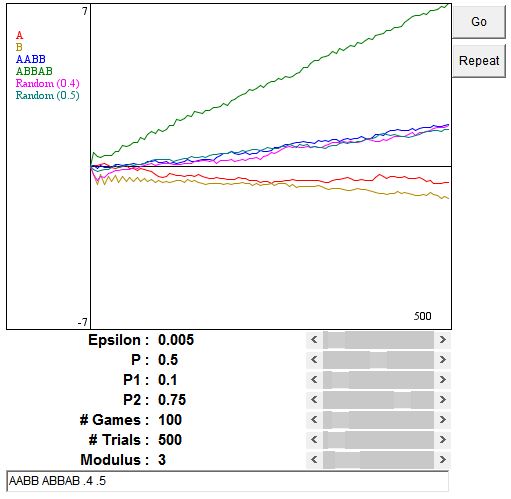
You may observe that the period ABBAB is by far the best strategy for
On the Web
- Brownian Motor, Franz-Josef Elmer, University of Basel (Java simulation)
- J. Havil, Nonplussed!, Princeton University Press, 2007
- Internet Bibliography of the Paradox by the inventor, Juan Manuel Rodriguez Parrondo
- Lee Spector's CGI Simulation (Hampshire College)
- Losing to Win, Ivars Peterson's MathTrek
- Paradox in Game Theory: Losing Strategy That Wins, Sandra Blakeslee, The NY Times On the Web Eastern Kentucky University (Java simulation)
(*) Erick Smith of Cayuga Pure Organics has observed in a private correspondence (December 14, 2007) that although "it may not matter at this point, but on your webpage on Parrando's Paradox, Brooke Buckley's analogy is not appropriate. Having sparrows and insects may, indeed, lead to having a better crop than either one by itself. But having both sparrows and insects is still worse than having neither. Thus having both is still a losing situation."
|Contact| |Front page| |Contents| |Probability|
Copyright © 1996-2018 Alexander Bogomolny
73511604
