Mutually (Jointly) Independent Events

Two events A and B are independent iff P(A∩B) = P(A)P(B). This definition extends to the notion of independence of a finite number of events. Let K be a finite set of indices. Events A_k, k∈K are said to be mutually (or jointly) independent iff

for any subset M⊂K. For example, for four events A, B, C, D to be mutually independent, we must have

Thus, by the definitions, mutual independence implies the pairwise independence. For two events, the definitions actually coincide. For more than two events, they are not. There are pairwise independent events that are not mutually independent. Two examples have been produced by S. N. Bernstein years ago and discussed more recently (2007) by C. Stepniak.

Consider an urn containing four balls, numbered 110, 101, 011 and 000, from which one ball is drawn at random. For k = 1, 2, 3 let A_k be the event of drawing a ball with 1 in the k^th position. Thus, the three events are pairwise independent. However, since A₁∩A₂∩A₃ = Ø, they are not mutually independent.

For a second example, let B_k be the event of drawing a ball with 0 in position k. Now, for k = 1, 2, 3, P(B_k) = 1/2, because in any of the three positions 0 appears exactly twice out of four possibilities. For any two distinct indices k and m, P(B_k∩B_m) = 1/4, for just one ball out of four has zeros both in positions k and m. Therefore, the events B_k are (pairwise) independent. However, P(B₁∩B₂∩B₃) = 1/4 which is different from P(B₁)P(B₂)P(B₃) = 1/8, meaning that the events are not mutually independent.

The two examples are essentially different because in the first the intersection of A's is empty whereas in the second the intersection of B's is not.

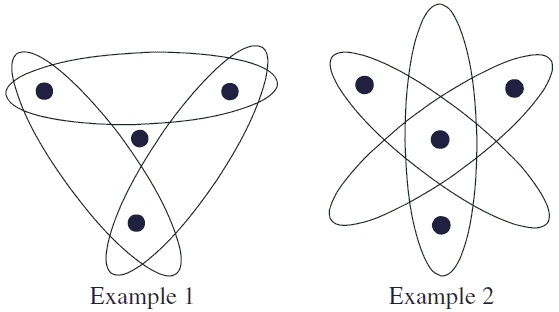
Noting this, Stepniak proceeds to prove that Bernstein's are the only possible examples in a space with four outcomes. Thus assume that three (pairwise) independent events A, B, C are defined in the space with four outcomes, none being the whole of the space. None may consist of a single outcome. For assume A = {x}. Then x may or may not belong to, say, B. If x∈B, then A∩B = A and P(A∩B) = P(A) ≠ P(A)P(B). On the other hand, if x∉B, A and B are disjoint and, therefore, are not independent. It follows, that each of the event contains at least two elements. Since the complements of two events are independent only of the events themselves are, we see that the complements of the events A, B, C also consist of at least 2 outcomes each. We conclude that each consists of exactly two outcomes.

There are just two possibilities. There is an outcome common to all three events, which gives the configuration of the second example. Or there is no outcome common to all events, which gives the configuration of the first example.

References

1. S. N. Bernstein, Theory of Probability, 4th ed. (in Russian), Gostechizdat, Moscow-Leningrad, 1946. (in Russian)
2. C. Stepniak, Bernstein’s Examples on Independent Events, The College Mathematics Journal, VOL. 38, NO. 2, MARCH 2007, 140-142

• What Is Probability?
• Intuitive Probability
• Probability Problems
• Sample Spaces and Random Variables
  • Importance of Having Sample Space Defined
• Probabilities
  • Example: A Poker Hand
  • Bernoulli Trials
  • Binomial Distribution
  • Proofreading Example
  • Continuous Sample Spaces
    • Geometric Probabilities
• Conditional Probability
  • Bayes' Theorem
    • Bayesian Odds
    • Bayes' Ratio: Dramatic Taxicab Example
    • Principle of Proportionality
• Dependent and Independent Events
  • Conditional Probability and Independent Events
  • Mutually (Jointly) Independent Events
  • Independent Events and Independent Experiments
• Algebra of Random Variables
• Expectation
• Probability Generating Functions
  • Sicherman Dice
• Random Walks
• Probabilistic Method

|Contact| |Front page| |Contents| |Up| |Store|

Copyright © `996-2010 Alexander Bogomolny