Geometric Probability

Random events that take place in continuous sample space may invoke geometric imagery for at least two reasons: due to the nature of the problem or due the the nature of the solution.

Some problems, like Buffon's needle, Birds On a Wire, Bertrand's Paradox, or the problem of the Stick Broken Into Three Pieces do, by their nature, arise in a geometric setting. The latter also admits multiple reformulations which require comparison of the areas of geometric figures. In general, we may think of geometric probabilities as non-negative quantities (not exceeding 1) being assigned to subregions of a given domain subject to certain rules. If function μ is an expression of this assignment defined on a domain D, then, for example, we require

0 ≤ μ(A) ≤ 1, A ⊂ D and
μ(D) = 1

The function μ is usually not defined for all A ⊂ D. Those subsets of D for which μ is defined are the random events that form a particular sample spaces. Very often μ is defined by means of the ratio of areas so that, if σ(A) is defined as the "area" of set A, then one may set μ(A) = σ(A) / σ(D).

Problem 1

Two friends who take metro to their jobs from the same station arrive to the station uniformly randomly between 7 and 7:20 in the morning. They are willing to wait for one another for 5 minutes, after which they take a train whether together or alone. What is the probability of their meeting at the station?

In a Cartesian system of coordinates (s, t), a square of side 20 (minutes) represents all the possibilities of the morning arrivals of the two friends at the metro station.

two friends meeting in metro

The gray area A is bounded by two straight lines, t = s + 5 and t = s - 5, so that inside A, |s - t| ≤ 5. It follows that the two friends will meet only provided their arrivals s and t fall into region A. The probability of this happening is given by the ratio of the area of A to the are of the square:

[400 - (15×15/2 + 15×15/2)] / 400 = 175/400 = 7/16.

Problem 2

([Sveshnikov, problem 3.12].)

Three points A, B, C are placed at random on a circle of radius 1. What is the probability for ΔABC to be acute?.

Fix point C. The positions of points A and B are then defined by arcs α and β extending from C in two directions. A priori we know that 0 < α + β < 2π. The favorable for our problem values of α and β (as subtending acute angles satisfy) 0 < α < π and 0 < β < π. Their sum could not be less than π as this would make angle C obtuse, therefore, α + β > π. The situation is presented in the following diagram where the square has the side 2π.

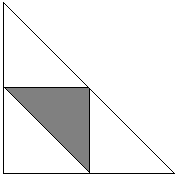
probability of a triangle being acute

Region D is the intersection of three half-planes: 0 < α, 0 < β, and α + β < 2π. This is the big triangle in the above diagram. The favorable events belong to the shaded triangle which is the intersection of the half-planes α < π, β < π, and α + β > π. The ratio of the areas of the two is obviously 1/4.

Now observe, that unless the random triangle is acute it can be thought of as obtuse since the probability of two of the three points A, B, C forming a diameter is 0. (For BC to be a diameter, one should have α + β = π which is a straight line, with zero as the only possible assignment of area.) Thus we can say that the probability of ΔABC being obtuse is 3/4. For an obtuse triangle, the circle can be divided into two halves with the triangle lying entirely in one of the halves. It follows that 3/4 is the answer to the following question:

Three points A, B, C are placed at random on a circle of radius 1. What is the probability that all three lie in a semicircle?

References

E. J. Barbeau, Murray S. Klamkin, W. O. J. Moser, Five Hundred Mathematical Challenges by (MAA, 1995, problem 244.)
D. A. Klain, G.-C. Rota Introduction to Geometric Probability , Cambridge University Press, 1997
A. A. Sveshnikov, Problems in Probability Theory, Mathematical Statistics and Theory of Random Functions, Dover, 1978
A. M. Yaglom, I. M. Yaglom, Challenging Mathematical Problems With Elementary Solutions, Dover, 1987

Geometric Probability

72111704