Naturally Discontinuous Functions
Most of the functions met by students in high school or in a Liberal Arts college are defined by analytic formulas:
Consider a billiard table in the shape of an equilateral triangle. Shoot a ball at a 60° angle to a side. After some journeying, the ball will close a polygonal loop and then trace the same polygon again. For all points on a side of the triangle but one, the loop is a hexagon whose perimeter does not depend on the position of the starting point. In the exceptional case, where we start in the middle of a side, the loop is a triangle with half the usual length.
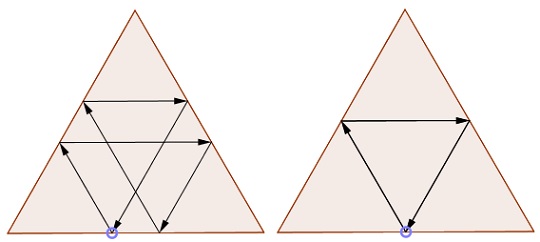
(For another example, see the Family Size page.)
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73585396
