Non-transitive Dice
The nontransitivity is a well known phenomenon which never fails to surprise the uninitiated and delight a professional. The nontransitivity refers to a situation with three or more alternatives in which this is impossible to choose the "most preferable" one because, whichever is chosen, there is always another one that beats it according to the prescribed rules of comparison. The Rock-Paper-Scissors game is sufficiently popular to use as a characteristic example.
A set of four nontransitive dice has been invented by Bradley Efron and described by Martin Gardner [Wheels, Time Travel, Mathematical Games, The Colossal Book] in the early 1970s in his Scientific American column. Efron's dice have been also described in the online references listed below. (The one by the James Grime is most entertaining. In addition to Eforn's 4-dice, you'll find there 3- and 7- nontransitive dice sets.)
As a new 2016 year surprise, I was informed of the discovery by Bráulio de O. Silveira from Brasil of seven sets of five nontransitive dice each. The complete result can be found in the pdf file. One of these sets is depicted in the following diagram:
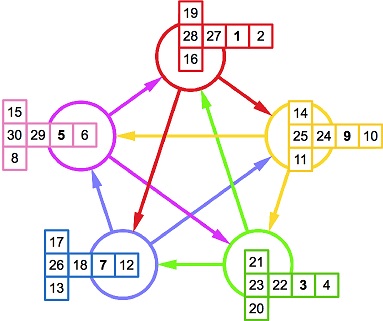
If the dice are designated by their smallest number, say, $(1),$ $(3),$ $(5),$ $(7),$ $(9),$ then as the diagram suggests $(1)\;$ beats $(9),\;$ $(9)\;$ beats $(3),\;$ $(3)\;$ beats $(7),\;$ $(7)\;$ beats $(5),\;$ and $(5)\;$ beats $(1).\;$ We write this concisely as $1\gt 9\gt 3\gt 7\gt 5\gt 1$ - all with the probability of $\displaystyle\frac{5}{9}.$ The sum of numbers on each of the dice is $93,$ and each of the seven sets uses all numbers from $1$ to $30$ and each exactly once.
There are also 3-dice loops, e.g., $1\gt 9\gt 3\gt 1,\;$ or $3\gt 7\gt 5\gt 3\;$ but no 4-dice loops. You can observe that on the diagram.
References
- J. Grime, Non-transitive Dice, singing banana
- Nontransitive Dice, wikipedia
- What is the most unfair set of three nontransitive dice?, math.stackexchange
- R. Honsberger, Some Surprises in Probability, in Mathematical Plums, by Ross Honsberger (editor), MAA, 1979
- Ed Pegg Jr., Tournament Dice, mathpuzzle, 7 Nov 2005
- M. Gardner, Nontransitive Paradoxes, in Time travel and other mathematical bewilderments, W H Freeman & Co, 1987
- M. Gardner, Nontransitive Dice and Other Probability Paradoxes, in Wheels, life, and other mathematical amusements, W H Freeman & Co, 1983
- M. Gardner, Directed Graphs and Cannibals, in The Last Recreations: Hydras,Eggs, and Other Mathematical Mystifications, Copernicus, 1997
- M. Gardner, Martin Gardner's Mathematical Games, MAA, 2005, (CDR)
- M. Gardner, The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems, W. W. Norton & Company, 286-311.
- What Is Probability?
- Intuitive Probability
- Probability Problems
- Sample Spaces and Random Variables
- Probabilities
- Conditional Probability
- Dependent and Independent Events
- Algebra of Random Variables
- Expectation
- Probability Generating Functions
- Probability of Two Integers Being Coprime
- Random Walks
- Probabilistic Method
- Probability Paradoxes
- Symmetry Principle in Probability
- Non-transitive Dice
|Contact| |Front page| |Contents| |Up|
Copyright © 1996-2007 Alexander Bogomolny
73511254
