Symmetry Principle in Probability
Problem
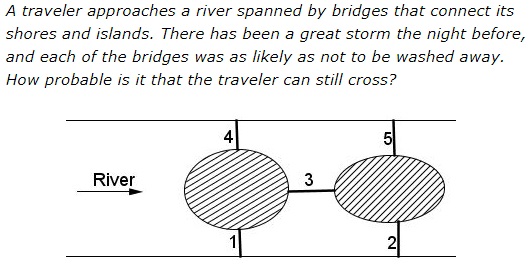
(This puzzle has been devised by Marcus Moore.)
In the absence of any additional (bridge structural and wear-and-tear) information, the traveler believes (and we will too) that all the bridges have equal probabilities and independent chances of being washed away.
Solution
The configuration of bridges has a remarkable symmetric structure.
Imagine that there is a boat floating down the stream. Any bridge that withstood the storm will block the passage of the boat. The boat will pass through if a sufficient number of bridges have been washed away. What is the probability that the boat will get through?
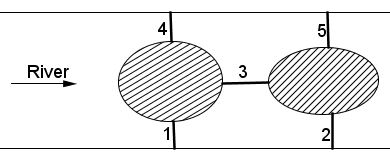
The key observation that brings a solution to the problem is that it has the same abstract structure for the traveler and the boat:

For the traveler, bridges 1 and 2 are the entries, whereas bridges 4 and 5 are exits. For the boat the entries are at bridges 1 and 4, the exits are at bridges 2 and 5.
A bridge that has withstood the storm is good for the traveler, but bad for the boat, and vice versa. But each individual event has the probability of $50\%.$ Having an identical abstract structure suggests the following observation. (Writing $P(X)$ for the probability of event $X):$
$P(\text{traveler crosses})=P(\text{Boat gets through}).$
But, beyond that, as we just observed, what is good for one is bad for the other, such that
$P(\text{boat gets through})=P(\text{traveler does not cross}).$
As a consequence of 1 and 2, we get
$P(\text{traveler crosses})=P(\text{traveler does not cross}),$
with the inevitable conclusion that both probabilities evaluate to $50\%.$
Context
I came across this problem in a chapter devoted to the concept of symmetry in Probability theory in a philosophy book Laws and Symmetry by Bas C. van Fraassen. To quote from the book:
Since its inception in the seventeenth century, probability theory has often been guided by the conviction that symmetry can dictate probability. The conviction is expressed in such slogan formulations as that equipossibility implies equal probability, and honoured by such terms as indifference and sufficient reason. As in science generally we can find here symmetry arguments proper that are truly a priori, as well as arguments that simply assume contingent symmetries, and 'arguments' that reflect the thirst for a hidden, determining reality. The great failure of symmetry thinking was found here, when indifference disintegrated into paradox; and great success as well, sometimes real, sometimes apparent. The story is especially important for philosophy, since it shows the impossibility of the ideal of logical probability.
The above problem serves an example where the assignment of equal probabilities (in the absence of any additional knowledge) seems justified and leads to a plausibly acceptable solution. However, this example (and equally successful application of symmetry for solving Buffon's Needle Problem) is followed by other examples that elucidate the difficulty the philosophers run into.
By the Principle of Symmetry, equal or uniform probabilities should be assigned to equipossible events. This becomes difficult, or even impossible, if the problem depends on more than one parameter, because, the uniformity of one parameter may conflict with uniformity of another. The book lists several such examples, Bertrand's paradox, in particular, some of which are very close to the one already discussed at this site.
Reference
- Bas C. van Fraassen, Laws and Symmetry, Oxford University Press, 1989
- What Is Probability?
- Intuitive Probability
- Probability Problems
- Sample Spaces and Random Variables
- Probabilities
- Conditional Probability
- Dependent and Independent Events
- Algebra of Random Variables
- Expectation
- Probability Generating Functions
- Probability of Two Integers Being Coprime
- Random Walks
- Probabilistic Method
- Probability Paradoxes
- Symmetry Principle in Probability
- Non-transitive Dice
![]()
|Contact| |Front page| |Contents| |Probability|
Copyright © 1996-2018 Alexander Bogomolny73582008
