Random Points on a Segment

When $n$ points are drooped on a unit segment, the distributions of lengths of the so obtained $n+1$ pieces are all the same.

To see why this indeed may be so, drop $n+1$ points on a circle. Then because of the symmetry, all the arcs so obtained have the same distribution. Now, tear the circle at one of the points. It must be true for the resulting segment with $n$ marked points that all its piece have the same length distribution.

Joshua Bowman has suggested that when $n=2$ calculations help realize the truth of the statement. Let the two points have coordinates $x$ and $y$. Then the expected value of the middle segment is

$\displaystyle\iint\limits_{[0,1]\times [0,1]}|x-y|dxdy=\frac{1}{3}.$

Let $L$ be the expected value of the length of the first piece. Since, according to the Symmetry Principle, the lengths of all three segments have the same distribution, their lengths have the same expected value, viz., $L.$ But in any experiment, the lengths of the three pieces add up to 1. It follows that $3L=1$ and $\displaystyle L=\frac{1}{3}.$

As in Problem 1, the expected value of each of the pieces - due to the Symmetry Principle - is $\displaystyle\frac{1}{2}.$ Not so for the expected value of the shorter of the two. (This is a curiosity because one of the two is surely shorter!)

If the point has landed on number $t$ then, provided $\displaystyle t\lt \frac{1}{2},$ the left piece is the shortest, otherwise, the shortest piece is on the right. Assuming it's the left one, its maximum length is $\displaystyle\frac{1}{2}$ and the average is half that, i.e., $\displaystyle\frac{1}{4}.$ The same number is found if $\displaystyle t\gt \frac{1}{2}.$ Then the average length of the longer piece is $\displaystyle\frac{3}{4},$ and the ratio of the two is $1:3.$ This is the ratio of the expected values. The expected value of the ratio is different.

Assume $\displaystyle t\gt \frac{1}{2}.$ Then $t$ is the length of the longer piece, $1-t$ is the length of the shorter one. Since $t$ is distributed uniformly on $\displaystyle [\frac{1}{2},1],$ the expected value of the ratio is

$\displaystyle 2\int_{\frac{1}{2}}^{1}\frac{1-t}{t}dt=2(\ln t - t)\bigg|_{\frac{1}{2}}^{1}=2\ln 2-1\approx 0.386.$

The expected value of the ratio of the longest segment to the shortest one is infinite, for it's equal to the divergent integral $\displaystyle 2\int_{\frac{1}{2}}^{1}\frac{t}{1-t}dt.$

As in Problem 1, the expected value of each of the pieces - due to the Symmetry Principle - is $\displaystyle\frac{1}{3}.$ However, if we talk of the expected values of the shortest, middle, and the longest segments, then all three numbers are different.

I'll use geometric insight. Assume that the left point is on distance $X$ from the left end, the right point on distance $Y,$ such that $X\lt Y.$ We can think of the pair $(X,Y)$ as being uniformly distributed in the unit square, with the condition $X\lt Y$ satisfied by the points above the main diagonal.

The task is to compare the three lengths: $X,$ $Y-X,$ and $1-Y.$ If $X$ is the least one, then $X\lt Y-X$ and $X\lt 1-Y,$ i.e., $2X\lt Y$ and $X+Y \lt 1.$ The area where the two conditions are satisfied is the dark triangle below:

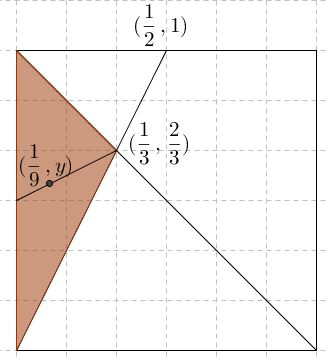
The average value of $X$ is attained at the center of gravity of the triangle, that is $\displaystyle\frac{1}{3}$ way from the base such that it is equal to $\displaystyle\frac{1}{3}\cdot\frac{1}{3}=\frac{1}{9}.$

Points $(X,Y)$ that correspond to the case where $X$ is the largest length lie in the quadrilateral marked below:

To find the average value of $X$ in the quadrilateral, it is split into two triangles. For the right triangle, the average value is $\displaystyle\frac{1}{2}+\frac{1}{6};$ for the left one, it is $\displaystyle\frac{1}{2}-\frac{1}{18}.$ The areas of the triangles are in proportion $3:1$ so that the average value of $X$ in the quadrilateral is the weighted sum:

$\displaystyle\frac{3\cdot (1/2+1/6)+1\cdot (1/2-1/18)}{3+1}=\frac{3\cdot 4/6+1\cdot 8/18}{4}=\frac{11}{18}.$

For the case, where $X$ is the middle length, we can shorten the computation, by subtracting from the total of $1$ the two fractions, $\displaystyle\frac{1}{9}=\frac{2}{18}$ and $\displaystyle\frac{11}{18}$ to obtain $\displaystyle\frac{5}{18}.$ It follows that the expected lengths of the shortest to the middle to the longest segments are in proportion $2:5:11.$

1. F. Mosteller, Fifty Challenging Problems in Probability with Solutions, Dover, 1987, problems 39-43