Conditional Probability and Independent Events

The applet below presents an interactive tool that helps grasp the definition and the significance of conditional probabilities and independent events.

If you are reading this, your browser is not set to run Java applets. Try IE11 or Safari and declare the site https://www.cut-the-knot.org as trusted in the Java setup.

What if applet does not run?

A sample space consists of an array of Nx × Ny dots. The dots are all equiprobable. Two rectangles represents two events, A and B, that can be moved or modified by dragging their sides or corners. Five probabilities are shown in the right side of the applet, P(A), P(B), P(A∩B), P(A|B), P(B|A). The latter two have been defined as

P(A|B) = P(A∩B) / P(B),
P(B|A) = P(A∩B) / P(A).

The events A and B are said to be independent provided

P(A|B) = P(A), or, which is the same
P(B|A) = P(B).

Neither the probability of A or B is affected by the occurrence (or a occurrence) of the other event. A symmetric way of expressing the same fact is this

P(A∩B) = P(A) P(B).

As an example, the events depicted below are independent on the 25×20 sample space:

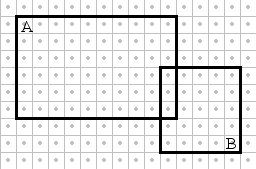
Independent events

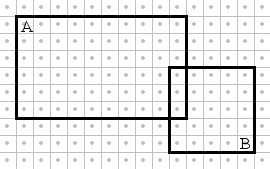
From the definition, for the dependency or independency of events the total frequencies of the events are as important as their relative frequencies. Switching (in the above example) to the sample space 24×20, say, but by keeping the relative probabilities P(A|B) and P(B|A) intact, turns the dependency on:

Dependent events

71931949