Matrices and Determinants as Optimization Tools: an Example
Leo Giugiuc, Dan Sitaru
February, 10, 2016
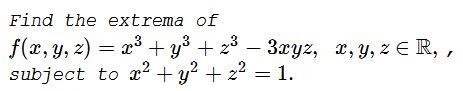
Solution
Let $A=\left(\begin{array}[ccc]\;x&y&z\\z&x&y\\y&z&x\end{array}\right).\;$ Obviously, $\det A=x^3+y^3+z^3-3xyz.\;$ On the other hand, $(\det A)^2=\det (AA^t)$ whereas
$AA^t=\left(\begin{array}\;x&y&z\\z&x&y\\y&z&x\end{array}\right)\left(\begin{array}\;x&z&y\\y&x&z\\z&y&x\end{array}\right) =\left(\begin{array}\;1&s&s\\s&1&s\\s&s&1\end{array}\right),$
where $s=xy+yz+zx\;$ such that $(\det A)^2=2s^3-3s^2+1=s^2(2s-3)+1.\;$ Clearly, $s^2\ge 0\;$ and, since
$s=xy+yz+zx\le x^2+y^2+z^2=1,$
$s^2(2s-3)\le 0\;$ and, subsequently $s^2(2s-3)+1\le 1.\;$ It follows that
$-1\le x^3+y^3+z^3-3xyz\le 1.$
Both bounds are achievable, for example, $f(-1,0,0)=-1\;$ and $f(1,0,0)=1,\;$ while $(\pm 1)^2+0^2+0^2=1.$
(A more traditional solution can be found on a separate page.)
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73606826
