An Inequality between AM, QM and GM
Problem
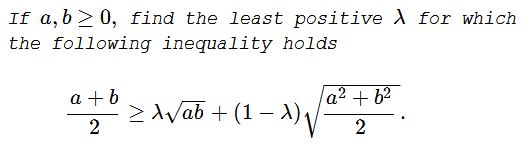
Solution 1
WLOG, $a+b=2.$ Set $a=1+\sqrt{\sin 2t}$ and $b=1-\sqrt{\sin 2t},$ $\displaystyle 0\le t\le\frac{\pi}{4}.$ We have:
$GM=\sqrt{1-\sin 2t}=\cos t-\sin t$ and
$QM=\sqrt{1+\sin 2t}=\cos t+\sin t,$
so that the inequality rewrites as
$1\ge\lambda (\cos t-\sin t)+(1-\lambda)(\cos t+\sin t),$
i.e., $2\lambda\sin t\ge \cos t+\sin t-1,$ for $\displaystyle t\in\left[0,\frac{\pi}{4}\right].$ Thus,
$\displaystyle \lambda\ge\max_{t\in\left[0,\frac{\pi}{4}\right]}\left(\frac{\cos t+\sin t-1}{2\sin t}\right)=\frac{1}{2}.$
Remark
It's easy to see that the function $f:\,\left[0,\frac{\pi}{4}\right]\,\rightarrow\,\left[1-\frac{1}{\sqrt{2}},\frac{1}{2}\right],$ defined by
$\displaystyle f(t)=\begin{cases} \displaystyle \frac{\cos t+\sin t-1}{2\sin t}, & \text{ if } t\int\in\left(0,\frac{\pi}{4}\right]\\ \displaystyle \frac{1}{2},& \text{ if }t=0 \end{cases}$
is continous, bijective and decreasing.
Thus, for a $\displaystyle\lambda\in\left[1-\frac{1}{\sqrt{2}},\frac{1}{2}\right),$ then there is $\displaystyle t\in\left(0,\frac{\pi}{4}\right]$ such that $\displaystyle \lambda\lt\frac{\cos t+\sin t-1}{2\sin t}.$ Setting $a=1+\sqrt{\sin 2t}$ and $b=1-\sqrt{\sin 2t},$ with that $t,$ we get
$\displaystyle \frac{a+b}{2}\lt\lambda\sqrt{ab}+(1-\lambda)\sqrt{\frac{a^2+b^2}{2}}.$
On the other hand, f $\displaystyle 0\lt\lambda\lt 1-\frac{1}{\sqrt{2}},$ then by setting, say, $a=2$ and $b=0,$ again
$\displaystyle \frac{a+b}{2}\lt\lambda\sqrt{ab}+(1-\lambda)\sqrt{\frac{a^2+b^2}{2}}.$
Solution 2
The problem: Find the smallest $\lambda \in [0,1]$ such that for all nonnegative $a,b$ the inequality
(1)
$\displaystyle \frac{a+b}{2} \geq \lambda \sqrt{ab} + (1-\lambda) \sqrt{\frac{a^2+b^2}{2}}$holds.
In my previous attempt I forgot what the problem was about and tried to find
$\min \left\{ \lambda(a,b) \mid a \neq b \geq 0\right\},$
which is not the same as
(2)
$\min \left\{ \lambda \mid \text{inequality (1) holds for all nonnegative } a\neq b \right\}$Here's a revised proof.
Define for nonnegative $a \neq b$
(3)
$\displaystyle \lambda(a,b) = \frac{\sqrt{\frac{a^2+b^2}{2}}-\frac{a+b}{2}}{\sqrt{\frac{a^2+b^2}{2}}-\sqrt{ab}}$which is the choice of $\lambda$ satisfying $\displaystyle \frac{a+b}{2} = \lambda \sqrt{ab} + (1-\lambda) \sqrt{\frac{a^2+b^2}{2}}.$
Note that the right-hand side of inequality (1) is decreasing in $\lambda$, so we can rewrite problem (3) as
$\begin{align} & \min \left\{ \lambda \mid \text{inequality (1) holds for all nonnegative } a\neq b \right\} \\=& \min \left\{ \lambda \mid \lambda \geq \lambda(a,b) \text{ for all nonnegative } a \neq b \right\} \\=& \sup \left\{ \lambda(a,b) \mid a \neq b \geq 0 \right\} \end{align}$
The answer is therefore the maximal value of $\lambda(a,b).$ Without loss we can assume $ab=1$, otherwise multiply numerator and denominator in (3) by $\frac{1}{\sqrt{ab}}$, which amounts to replacing $a,b$ by $\frac{a}{\sqrt{ab}}, \frac{b}{\sqrt{ab}}.$
$\begin{align} \lambda(a,b) &= \frac{\sqrt{\frac{a^2+a^{-2}}{2}}-\frac{a+a^{-1}}{2}}{\sqrt{\frac{a^2+a^{-2}}{2}}-1} \\&= \frac{\sqrt{\cosh(2t)} - \cosh(t)}{\sqrt{\cosh(2t)}-1} \qquad (e^t = a) \\&= \frac{\sqrt{2\cosh^2(t)-1} - \cosh(t)}{\sqrt{2\cosh^2(t)-1}-1} \\&= \frac{\sqrt{2s^2-1} - s}{\sqrt{2s^2-1}-1} \qquad (s = \cosh(t) > 1) \end{align}$
The last term is decreasing in $s$ and reaches its supremum at $s \searrow 1$, hence the optimal choice is
$\displaystyle \begin{align} \lambda = \displaystyle\lim_{s\searrow 1} \frac{\sqrt{2s^2-1} - s}{\sqrt{2s^2-1}-1} &= \displaystyle\lim_{s\searrow 1} \frac{\frac{2s}{\sqrt{2s^2-1}} - 1}{\frac{2s}{\sqrt{2s^2-1}}} \qquad (\text{L'Hôpital's rule}) \\&= \displaystyle\lim_{s\searrow 1} \frac{2s-\sqrt{2s^2-1}}{2s} \\&= \displaystyle\lim_{s\searrow 1} \frac{2-\sqrt{2-s^{-2}}}{2} \\&= \frac{1}{2} \end{align}$
Solution 3
In polar coordinates $(0 \leq u \leq \frac {\pi}{2})$ we have
$\displaystyle r\cos(u)+r\sin(u) \geq 2 \lambda r \sqrt {\sin(u)\cos(u)}+ (1-\lambda)r\sqrt{\frac{1}{2}}$
We can eliminate $r$ to obtain
$\displaystyle \cos(u)+\sin(u)- \sqrt{2} \geq \lambda(2\sqrt{\cos(u)\sin(u)}-\sqrt{2}) $
where $\displaystyle \forall u, u\neq \frac{\pi}{4}\Rightarrow (2\sqrt{\cos(u)\sin(u)}-\sqrt{2}) \lt 0 $
and so we are looking for the least positive so that
$\displaystyle F(u) = \frac{\cos(u)+\sin(u)- \sqrt{2}}{2\sqrt{\cos(u)\sin(u)}-\sqrt{2}}\leq\lambda $
We have $ \forall u \Rightarrow F(u) \geq 0$ and that the number we are looking for is max of $F(u)$ in $\displaystyle 0\leq u \leq \frac{\pi}{2} $
We set $p=\sqrt{\cos(u)\sin(u)}$ and $\displaystyle \bar{p}= \sqrt{\frac{1}{2}}(\Rightarrow \bar{u}= \frac{\pi}{4}).$ Then, with substitution, we must find max of $F(p)$ where
$\displaystyle F(p) = \frac {\sqrt{1+2p^2}-\sqrt{2}}{2p-\sqrt{2}},$ $\displaystyle 0 \leq p < \sqrt{\frac{1}{2}}$
Now, by de l'Hôpital's rule,
$\displaystyle \lim_{p\to\bar{p}}{\frac{\sqrt{1+2p^2}-\sqrt{2}}{2p-\sqrt{2}}}= \frac{1}{2} $
Consider now
$\displaystyle \begin{align} F(p)-\frac{1}{2}&= \frac{2\sqrt{1+2p^2}-(2p+\sqrt{2})}{4p-2\sqrt{2}}\\ &= \frac{2\sqrt{1+2p^2}-(2p+\sqrt{2})}{4p-2\sqrt{2}}\cdot\frac{2\sqrt{1+2p^2}+(2p+\sqrt{2})}{2\sqrt{1+2p^2}+(2p+\sqrt{2})}\end{align}$
and note that numerator can be written as $4p^2-4\sqrt{2}+2=2(\sqrt{2}-1)^2\ge 0,$ whereas the denominator is always negative for $\displaystyle 0\le p\lt\sqrt{\frac{1}{2}}.$ Thus, $\displaystyle F(p)\le\frac{1}{2}$ and $\lim_{p\rightarrow\bar{p}}{F(p)}=\frac{1}{2}$ and so $\max F(p)=\frac{1}{2}=least\;\lambda.$
Acknowledgment
Leo Giugiuc has kindly communicated to me the above problem, along with a solution of his. According to Kadir Altintas, the problem was offerred at the 2017 Hong Kong math olympiad. The remark is also by Leo and came up during a discussion on other solutions of the problem. Solution 2 is by Long Huynh Huu; Solution 3 is by Andrea Acquaviva.
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73564059
