Extremal Problem in a Circular Segment

The following simple problem has been included in two of Ross Honsberger's books. In the Mathematical Morsels he gave a solution by C. M. Ingleby and later in Mathematical Gems III added two more solutions, one by I. van Yzeren and the other by Karel A. Post. The three solution are given below. More recently, M. Hajja published 3 short trigonometric proofs and pointed to the relation of the diagram in the first solution below to the Broken Chord Theorem. The fourth solution on this page exploits Hajja's observation.

P is a variable point on the arc of a circle cut off by the chord AB.

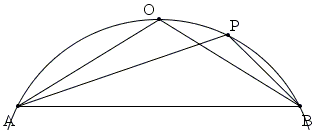
sum of two chords

Prove the intuitively obvious property that the sum of the chords AP and BP is a maximum when P is at the midpoint O of the arc AB.

Solutions

References

  1. M. Hajja, Another Morsel of Honsberger, Math. Magazine VOL. 83, NO. 4, OCTOBER 2010, 279-283
  2. R. Honsberger, Mathematical Morsels, MAA, 1978, pp. 16-17
  3. R. Honsberger, Mathematical Gems III, MAA, 1985, pp. 22-24

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

Solution 1

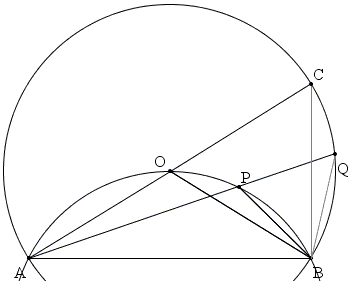
sum of two chords, proof 1

With center O draw a circle through A and B and extend AO to AC and AP to AQ, with C and Q on the circle.

AO = BO = CO,

implying that

∠AOB = 2 ∠ACB (= 2 ∠OBC.)

On the other hand, ∠APB = ∠AOB and ∠AQB = ∠ACB. Thus,

∠APB = 2 ∠AQB.

But, as an exterior angle of ΔBPQ, ∠APB = ∠AQB + ∠OBQ, so that ∠OBQ = ∠AQB, making ΔBPQ isosceles:

BP = PQ.

It follows that AQ = AP + PQ and AC = AO + CO. Both AQ and AC are chords in the extra circle, with AC being a diameter, the longest chord: AQ < AC.

Solution 2

Let K be the center of the circle (with arc AOB). Draw KE, the bisector of ∠AKP and KF, the bisector of ∠PKB and add EL ⊥ KP and FM ⊥ KP. If W is the point of intersection of AP and KE, then KW ⊥ AP and AW = PW.

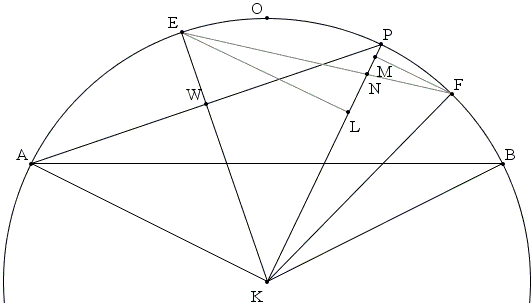
sum of two chords, proof 2

By symmetry, PW = EL. Hence, EL = AP/2. Similarly, FM = BP/2. Let N be the intersection of KP and EF. Triangles ELN and FMN are right. Their hypotenuses exceed their legs: EN > AL and FM > FN. Adding up

(AP + BP) / 2 = EL + FM > EN + FN = EF.

But ∠EKF = ½∠AKB = ∠AKO = ∠OKB, making the subtending chords equal:

EF = AO = BO.

Finally, (AP + BP) / 2 > EF = (AO + BO) / 2.

Solution 3

Let X be the intersection of AP and BO.

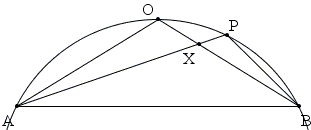
sum of two chords, proof 3

Triangles AOX and BPX are equiangular and, thus, similar. With P between O and B, ΔAOX is the larger of the two:

AO/BP = AX/BX = OX/PX = k > 1.

We are concerned with the difference (AO + BO) - (AP + BP):

 (AO + BO) - (AP + BP)= (AO + OX + BX) - (AX + PX + BP)
  = (AO + OX - AX) - (PX + BP - BX)
  = (kBP + kPX - kBX) - (BP + PX - BX)
  = (k - 1)(BP + PX - BX) > 0,

by the triangle inequality.

Solution 4

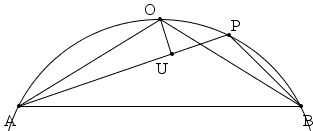
sum of two chords, proof 4

Let U be the foot of the perpendicular from O to AP. By the broken chord theorem 2·AU = AP + BP. In the right triangle AOU, AO serves as hypotenuse and, therefore, AO ≥ AU. It follows that

AO + BO = 2·AO ≥ 2·AU = AP + BP.

References

  1. M. Hajja, Another Morsel of Honsberger, Math. Magazine VOL. 83, NO. 4, OCTOBER 2010, 279-283
  2. R. Honsberger, Mathematical Morsels, MAA, 1978, pp. 16-17
  3. R. Honsberger, Mathematical Gems, III, MAA, 1985, pp. 22-24

The Broken Chord Theorem

  1. The Broken Chord Theorem: Proof Close to Archimedes'
  2. The Broken Chord Theorem: proof by Gregg Patruno
  3. The Broken Chord Theorem by Paper Folding
  4. The Broken Chord Theorem: proof by Stuart Anderson
  5. The Broken Chord Theorem: proof by Bui Quang Tuan
  6. The Broken Chord Theorem: proof by Mariano Perez de la Cruz
  7. Pythagoras' from the Star of David
  8. Pythagoras' from Broken Chords
  9. Extremal Problem in a Circular Segment

Related material
Read more...

A Sample of Optimization Problems

  • Mathematicians Like to Optimize
  • Reshuffling knights - castle defenders
  • Isoperimetric Theorem and Inequality
  • Viewing a Statue: the Problem of Regiomontanus
  • Fagnano's Problem
  • Minimax Principle Demonstration
  • Maximum Perimeter Property of the Incircle
  • Optimization in Four Variables with Two Constraints
  • Daniel Dan's Optimization in Three Variables
  • Problem in a Special Trapezoid
  • Cubic Optimization with Linear Constraints
  • Cubic Optimization with Partly Linear Constraints
  • Problem M317 from Crux Mathematicorum
  • Find the Maximum and Minimum of a Function
  • Area of Isosceles Triangle
  • Minimum of Cotangents from Saint Petersburg

    • |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    71941698