The Broken Chord Theorem
Proof by Mariano Perez de la Cruz
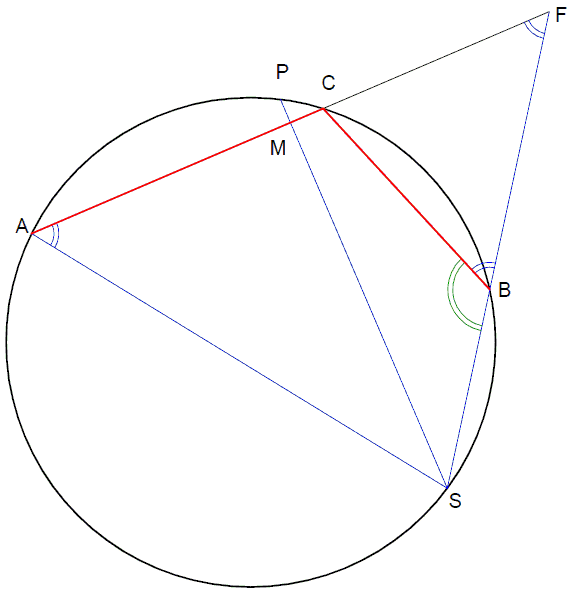
On the circumcircle of triangle ABC, point P is the midpoint of the arc ACB. PM is perpendicular to the longest of AC or BC. Prove that M divides the broken line ACB in half.
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
On the circumcircle of triangle ABC, point P is the midpoint of the arc ACB. PM is perpendicular to the longest of AC or BC. Prove that M divides the broken line ACB in half.

By extending PM to its intersection with the circumference we get point S. A line from S through B intersects the AC extended in F.
∠MSA = ∠MSF since P bisects the original arc AB, implying
We are to prove that CF = CB.
This is so because, ∠CBF is suplementary of ∠CBS, and, since ACBS is an inscribed quadrilateral, ∠CAS =
∠CFB, both being suplementary to ∠CBS. Therefore
The Broken Chord Theorem
- The Broken Chord Theorem: Proof Close to Archimedes'
- The Broken Chord Theorem: proof by Gregg Patruno
- The Broken Chord Theorem by Paper Folding
- The Broken Chord Theorem: proof by Stuart Anderson
- The Broken Chord Theorem: proof by Bui Quang Tuan
- The Broken Chord Theorem: proof by Mariano Perez de la Cruz
- Pythagoras' from the Star of David
- Pythagoras' from Broken Chords
- Extremal Problem in a Circular Segment
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73580450
