Minimum of Cotangents from Saint Petersburg
Problem
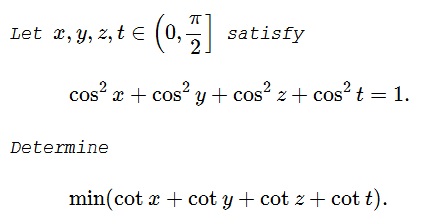
Solution
Set $a=\cos^2x,$ $b=\cos^2y,$ $c=\cos^2z,$ $d=\cos^2t.$ First of all, $a,b,c,d\in [0,1),$ and $a+b+c+d=1.$
Clearly,
$\displaystyle \cot x+\cot y+\cot z+\cot t=\sqrt{\frac{a}{1-a}}+\sqrt{\frac{b}{1-b}}+\sqrt{\frac{c}{1-c}}+\sqrt{\frac{d}{1-d}}.$
As we found previously, $\displaystyle \sqrt{\frac{a}{1-a}}+\sqrt{\frac{b}{1-b}}+\sqrt{\frac{c}{1-c}}+\sqrt{\frac{d}{1-d}}\ge 2.$
Equality is attained for $\displaystyle (a,b,c,d)=\left(\frac{1}{2},\frac{1}{2},0,0\right)$ and permutations. Thus the sought minimum equals $2.$
Acknowledgment
This is problem 3 from the 2017 Saint Petersburg (Russia) Mathematical Olympiad. Leo Giugiuc has kindly communicated to me the problem along with his solution.
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
73580804
