Cubic Optimization with Partly Linear Constraints
Problem
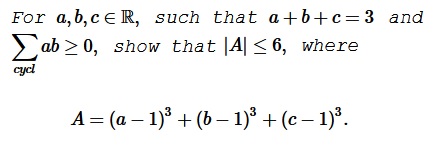
Solution 1
We reformulate the problem:
For $x,y,z\in\mathbb{R},\,$ such that $x+y+z=0\,$ and $\displaystyle\sum_{cycl}xy\ge -3,\,$ find maximum of $|x^3+y^3+z^3|.$
Let $xy+yz+zx=-3q^2,\,$ with $q\ge 0.\,$ Since $-3q^2\ge -3,\,$ $q\le 1.$
Also, $x^3+y^3+z^3=3xyz.\,$ Since it has three real roots, it follows from the Cardano-Tartaglia formula, that $|xyz|\le 2q^2.\,$ It follows that $|x^3+y^3+z^3|\le 6q^2.\,$ Taking into account $q\le 1,\,$ $|x^3+y^3+z^3|\le 6.\,$ Equality is attained at the permutations of $(\pm 1,\pm 1, \mp 2).$
Solution 2
We follow the Vo Quoc Ba Can's theory: $\displaystyle\sum_{cycl}ab-\frac{p^2-q^2}{3}=\frac{9-q^2}{3}\ge 0,\,$ implying $0\le q\le 3.\,$ As usual, $r=abc.\,$ For the reference's sake, here's the VQBC inequality, adapted to our case of $a+b+c=3:$
$\displaystyle \frac{(3+q)^2(3-2q)}{27}\le r\le \frac{(3-q)^2(3+2q)}{27}.$
$\displaystyle\sum_{cycl}(a-1)=0\,$ implies
$\begin{align} A &= \sum_{cycl}(a-1)^3=3(a-1)(b-1)(c-1)\\ &= 3(r-\sum_{cycl}ab+2). \end{align}$
Thus,
$\begin{align} \frac{A}{3} &\le \frac{(3-q)^2(3+2q)}{27}-\frac{9-q^2}{3}+2\\ &= \frac{2q^3}{27}\le\frac{2}{27}3^3=2, \end{align}$
so that $A\le 6.\,$ Equality holds for $q=3,\,$ and $\displaystyle\sum_{cycl}ab=0,\,$ i.e. $(a,b,c)=(3,0,0)\,$ and permutations hereof. On the other hand,
$\begin{align} \frac{A}{3} &\ge \frac{(3+q)^2(3-2q)}{27}-\frac{9-q^2}{3}+2\\ &= -\frac{2q^3}{27}\ge -\frac{2}{27}3^3=-2, \end{align}$
so that $A\ge -6.\,$ Equality holds at $q=3,\,$ where $r=-4\,$ and $\displaystyle\sum_{cycl}ab=0,\,$ implying $(a,b,c)=(2,2,-1)\,$ and permutations.
Illustration
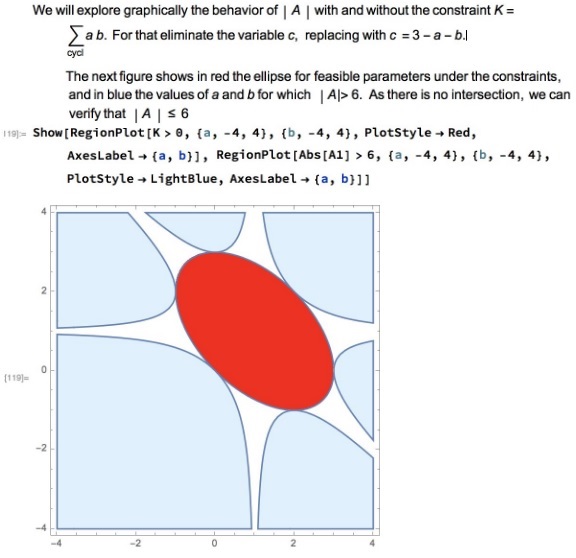
Acknowledgment
After solving Marian Dincă's problem, Imad Zak came up with the above modification. Solution 1 is by Leo Giugiuc; Solution 2 is by Imad Zak. The illustartion is by N. N. Taleb.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73583965
