Problem in a Special Trapezoid
Problem

Solution 1
Let $x\,$ denote the angle $CAE.$
We'll recourse to complex numbers. WLOG, let $A=0,\,$ $B=i,\,$ $D=1,\,$ $C=k+i,\,$ with $k\gt 0.\,$ Then $E=mk+1-m+mi,\,$ $0\lt m\lt 1.\,$
We have $\displaystyle\frac{2}{3}=\tan\alpha=\frac{im\left(\frac{C-B}{E-B}\right)}{re\left(\frac{C-B}{E-B}\right)},\,$ so that $\displaystyle m=\frac{1}{2k+1}\,$ and $E=\displaystyle\frac{3k+i}{2k+1}.\,$ Also $\displaystyle\tan x=\frac{im\left(\frac{C-A}{E-A}\right)}{re\left(\frac{C-A}{E-A}\right)}=\frac{2k}{3k^2+1}.\,$
Clearly, $\displaystyle\frac{2k}{3k^2+1}\le\frac{1}{\sqrt{3}}.\,$ with equality iff $k=\displaystyle\frac{1}{\sqrt{3}},\,$ i.e., when $x=30^{\circ}.\,$ Thus, $\max x=30^{\circ}.$
Solution 2
With a reference to the diagram below, the equation of line $r\,$ is $y=1-\displaystyle\frac{2x}{3},\,$ whereas the equation of line $s\,$ is $y-\displaystyle\frac{1-x}{1-k}.\,$ Point $E=t\cap s,\,$ $E=\displaystyle\left(\frac{3k}{2k+1},\frac{1}{2k+1}\right).$
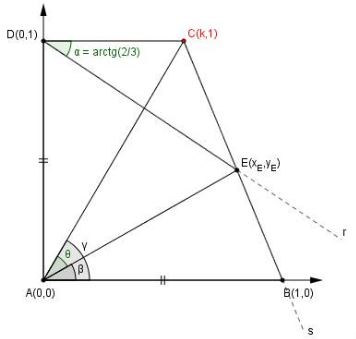
$\tan\beta=\displaystyle\frac{1}{3k},\,$ $\tan\gamma=\displaystyle\frac{1}{k}.\,$
$\theta=\gamma-\beta,\,$ such that $\displaystyle\tan\theta=\frac{\tan\gamma-\tan\beta}{1+\tan\gamma\cdot\tan\beta}=\frac{2k}{3k^2+1}.$
Since $\displaystyle\frac{3k^2+1}{2k}=\frac{3k}{2}+\frac{}{2k},\,$ the AM-GM inequality gives $\displaystyle\frac{3k^2+1}{2k}\ge 2\sqrt{\frac{3k}{2}\cdot\frac{1}{2k}},\,$ from which $m\ge\sqrt{3},\,$ $\displaystyle\tan\theta\le\frac{1}{\sqrt{3}},\,$ meaning that $\displaystyle\max \tan\theta=\frac{1}{\sqrt{3}}.\,$ That means that $\max\theta=30^{\circ}.$
Remark
Knowledge of $k,$ for the optimal angle, allows us to make additional observation, concerning the configuration. For, one $\displaystyle\tan\angle BAC=\frac{k}{1}=\frac{1}{\sqrt{3}},\,$ implying that $\angle BAC=30^{\circ}\,$ such that, also, $\angle DAE=30^{\circ}.\,$ We see that, at the optimal configuration, lines $AC\,$ and $AE\,$ trisect $\angle BAD.$
Acknowledgment
The problem from the Peru Geometrico group has been kindly posted by Leo Guigiuc at the CutTheKnotMath facebook page. The problem by Franzua Ynfanzon has been posted at the Peru Geometrico group by Elberling Vargas Diaz; Solution 1 is by Leo Giugiuc; Solution 2 is by Marco Antônio Manetta.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579768
