Problem M317 from Crux Mathematicorum
What Is This About?
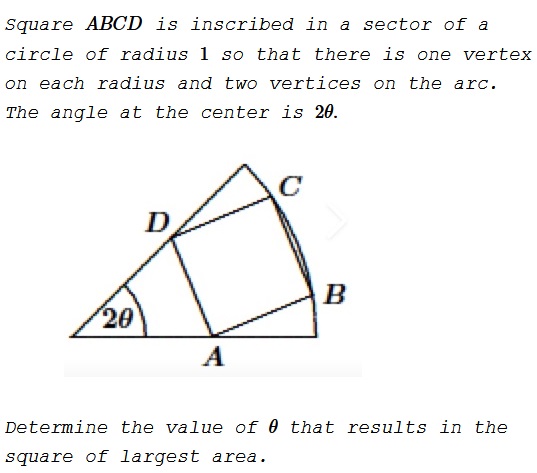
Problem
Solution 1
We assume that $2\theta$ is proper, i.e. $\displaystyle \theta\in\left(0,\frac{\pi}{2}\right).$ Consider the circle $\omega:\;x^2+y^2=1,$ with center $O.$ Choose $A=k-mki$ and $D=t+mti,$ where $m=\tan\theta$ and $0\lt k,t\lt\displaystyle \frac{1}{\sqrt{1+m^2}}.$ Let's find $B$ and $C$ such that the square $ABCD$ is positively oriented. We have: $\displaystyle \frac{C-D}{A-D}=i,$ from which $C=t+m(t+k)+(mt-t+k)i.$
Since $B=A+C-D,$ we find that $B=k+m(t+k)+(-mk-t+k)i.$ But $B,C\in \omega,$ implying
$[t+m(t+k)]^2+[mt-t+k]^2=1\\ [k+m(t+k)]^2+[-mk-t+k]^2.$
So that, by subtraction, $(1+m^2)(t-k)(t+k)=0$ so that $t=k.$ With $t=k,$ the two equations reduce to $t^2(1+4m+5m^2)=1.$ It follows that $\displaystyle AB=\frac{2m}{\sqrt{5m^2+4m+1}},$ and $\displaystyle [ABCD]=\frac{4m^2}{5m^2+4m+1}.$
The function $\displaystyle f(m)=\frac{4m^2}{5m^2+4m+1}$ is strictly increasing on $(0,\infty).$ From which we deduce that, for $\displaystyle \theta\in\left(0,\frac{\pi}{2}\right),$ $\displaystyle [ABCD]\lt\frac{4}{5}.$ Now, for $\displaystyle \theta=\frac{\pi}{2},$ $\displaystyle AB=\frac{2}{\sqrt{5}},$ i.e, $\displaystyle [ABCD]=\frac{4}{5}.$
The required value of $\theta$ is $\displaystyle \frac{\pi}{2}.$
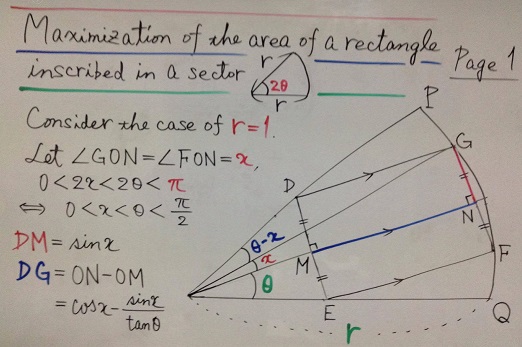
Solution 2


Acknowledgment
The problem was posted at the Crux Mathematicorum facebook site and kindly brought to my attention by Leo Giugiuc, along with his solution (Solution 1). Solution 2 is by Kunihiko Chikaya delivered through the facebook messenger.
The problem has been proposed by Bruce Shawyer, Memorial University of Newfoundland, St. John's, NL, Canada.
Remark
Note that when $\displaystyle \theta\gt\frac{\pi}{2},$ the sector ceases to be convex, although, for $\displaystyle \theta\in\left(\frac{\pi}{2},\frac{3\pi}{4}\right),$ a square still exists with two vertices on the sector's radii and two vertices on the arc. At $\displaystyle \theta=\frac{3\pi}{4},$ the square becomes inscribed in the circle, and, therefore, is maximally possible under these condintions.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73565166
