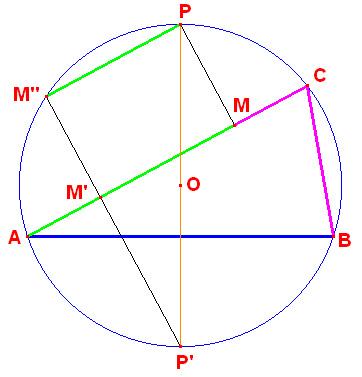
On the circumcircle of triangle ABC, point P is the midpoint of the arc ACB. PM is perpendicular to the longest of AC or BC. Prove that M divides the broken line ACB in half.
On the circumcircle of triangle ABC, point P is the midpoint of the arc ACB. PM is perpendicular to the longest of AC or BC. Prove that M divides the broken line ACB in half.
Let O denote the circumcenter of ΔABC. P' = symmetry of P in O. Because P is midpoint of arc ACB so PP' is perpendicular bisector of AB and P, C are on one side with respect to AB.
The perpendicular from P' to AC cuts AC at M' and cuts the circumcircle (O) again at M''. Two angles CAB and M''P'P are equal because their side lines are respectively perpendicular. Hence their subtending chords are also equal:
CB = M''P = M'M.
By symmetry of circumcircle, CM = AM'. From these:
AM = AM' + M'M = MC + CB
And the proof is complete.
The Broken Chord Theorem
- The Broken Chord Theorem: Proof Close to Archimedes'
- The Broken Chord Theorem: proof by Gregg Patruno
- The Broken Chord Theorem by Paper Folding
- The Broken Chord Theorem: proof by Stuart Anderson
- The Broken Chord Theorem: proof by Bui Quang Tuan
- The Broken Chord Theorem: proof by Mariano Perez de la Cruz
- Pythagoras' from the Star of David
- Pythagoras' from Broken Chords
- Extremal Problem in a Circular Segment
|Activities|
|Contact|
|Front page|
|Contents|
|Geometry|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
