Pythagoras' from Broken Chords

Bui Quang Tuan found a way to derive the Pythagorean Theorem from the Broken Chord Theorem.

Let ABC be a triangle with a right angle at C, AB is diameter of circumcircle (O). If P is the midpoint of the arc ACB, the APB is right isosceles triangle, with the right angle at P. Assuming AC > BC, let M be the orthogonal projection of P on AC. Line PM cuts AB at N, B' is orthogonal projection of B on PM, as in the diagram:

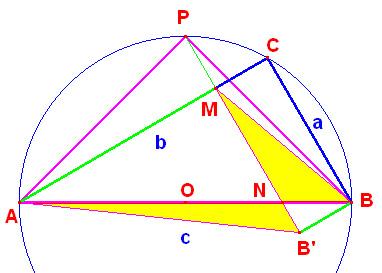
As usual, let a = BC, b = AC, c = AB.

Since BCMB' is rectangle,

By the Broken Chord Theorem,

And, since PMC is right isosceles triangle at M,

Further,

because AM||B'B.

Now, the area of APB equals c²/4. We find it yet in a different way:

Using (1), (2), (3), (4) to calculate areas of triangles, we obtain:

This means c²/4 = (a² + b²)/4 or c² = a² + b². The proof is complete.

The Broken Chord Theorem

1. The Broken Chord Theorem: Proof Close to Archimedes'
2. The Broken Chord Theorem: proof by Gregg Patruno
3. The Broken Chord Theorem by Paper Folding
4. The Broken Chord Theorem: proof by Stuart Anderson
5. The Broken Chord Theorem: proof by Bui Quang Tuan
6. The Broken Chord Theorem: proof by Mariano Perez de la Cruz
7. Pythagoras' from the Star of David
8. Pythagoras' from Broken Chords
9. Extremal Problem in a Circular Segment

|Contact| |Front page| |Contents| |Geometry| |Pythagorean Theorem| |Store|