Pythagoras' from the Star of David

The following proof of the Pythagorean theorem is due to Stuart Anderson (September 17, 2010).

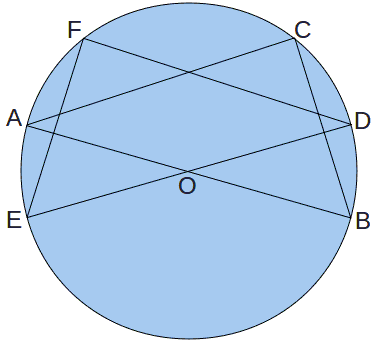
Let a pair of mirror congruent right triangles ABC and DEF be inscribed in a circle with diameters AB and DE, so that DE is perpendicular to BC. (By symmetry, AB is perpendicular to EF.) Then DE bisects BC and its major arc, and likewise AB bisects EF and its major arc.

Then by the Broken Chord Theorem, EF cuts AB into parts (AB + AC)/2 and (AB - AC)/2, and by the Intersecting Chords Theorem,

Therefore, AB² - AC² = BC², which is the Pythagorean Theorem.

The Broken Chord Theorem

1. The Broken Chord Theorem: Proof Close to Archimedes'
2. The Broken Chord Theorem: proof by Gregg Patruno
3. The Broken Chord Theorem by Paper Folding
4. The Broken Chord Theorem: proof by Stuart Anderson
5. The Broken Chord Theorem: proof by Bui Quang Tuan
6. The Broken Chord Theorem: proof by Mariano Perez de la Cruz
7. Pythagoras' from the Star of David
8. Pythagoras' from Broken Chords
9. Extremal Problem in a Circular Segment

|Contact| |Front page| |Contents| |Geometry| |Pythagorean theorem| |Store|