Isoperimetric Theorem and Inequality
Isoperimetric Theorem has been known from the time of antiquity. Elegant all by itself, the Theorem also has a fascinating history. The most essential contribution towards its rigorous proof was given in 1841 and is due to Jacob Steiner (1796-1863). At the time it stood at the center of controversy between adherents of analytic (i.e. using Calculus) and synthetic (pure Geometric) methods. Although accepting validity of the analytic methods, Steiner only used synthetic approach. His proof contained a flaw that later was fixed by analytic approach. To better understand the nature of the discussion let me first formulate two equivalent statements. The Isoperimateric Theorem deals with the area and perimeter (circumference) of circle:
Statement 1
Among all planar shapes with the same perimeter the circle has the largest area.
Statement 2
Among all planar shapes with the same area the circle has the shortest perimeter.
Theorem
The two Statements 1 and 2 are equivalent.
Proof
As a shorthand, denote Statement 1 as A and Statement 2 as B. Assume A holds and let us prove B. Suppose, on the contrary, that B is false. Then for a given circle C there exists a figure F with the same area but with a perimeter shorter than that of C. Shrink C into a smaller circle C' whose perimeter equals that of F. The area of C' will clearly be smaller than that of C and, consequently, it will be smaller than the area of F. Now, this contradicts our assumption that A holds: C' and F have the same perimeter but the area of the circle C' is less than the area of F.
The implication B ⇒ A is proven in precisely the same fashion. Q.E.D.
Note that we did not prove either A or B but rather that they are either both true or both false. Mathematical theorems in general have premises and conclusions and assert that the latter follow from the former. Human reasoning often resorts to the well known modus ponens syllogism: if A=>B and A are true then so is B. Oftentimes, the premise A seems to be so obviously true that a proof of A=>B is mistakenly substituted for a proof of B.
See if you can detect an inconsistency in the following
Proof of Statement 1

The proof will proceed in several steps. First of all, let us note that the figure that solves
Statement 1 (we hope it's a circle) must be convex. Indeed, assume it's not (see Fig 1).
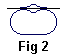 This would imply
existence of two points from the figure such that the connecting segment would not itself lie inside
our shape. Then reflecting a region between the segment and the boundary of the shape
as on Fig. 2, it would be possible to increase its area without modifying its perimeter.
This would imply
existence of two points from the figure such that the connecting segment would not itself lie inside
our shape. Then reflecting a region between the segment and the boundary of the shape
as on Fig. 2, it would be possible to increase its area without modifying its perimeter.
On the second step we proof the following
Lemma 1
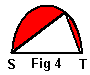
Let two points S and T be selected on the boundary of the shape solving Statement 1 such that the points divide the perimeter into two equal parts. Then the segment ST must divide the area of the shape into two equal parts.

Proof of Lemma 1
Assume, on the contrary, the area S1T is larger than T2S (Fig 3). Then reflecting S1T in ST will get the shape S1T3 with the same perimeter as S1T2 but a larger area.
From this proof it appears that it's sufficient to solve the following "half" of the problem: Among all arcs with a given length and endpoints on a line ST find the one that along with the line ST encloses the largest area. This question was previously posed elsewhere on this site.
Lemma 2
Consider all the arcs with a given length and the endpoints S and T on a fixed straight line. The curve that encloses the maximum area between the curve and the straight line is a semicircle.
Proof of Lemma 2
Suffice it to show that every angle inscribed into the arc is right. If there is a point on the arc, say P, for which ∠SPT is not right, slide either point S or point T along the straight line ST until the angle becomes right. Let pieces of the arc move along. As an exercise prove that among all triangles with two given sides the one whose sides enclose a right angle has the largest area.  Since the area of the two red regions did not change but the area of the triangle (Fig 5) grew, the whole area between the new curve SPT and the line ST has increased. This shows that unless the curve is a semicircle we can always increase the area in question by moving points S and T. This proves Lemma 2 and with it Statement 1.
Since the area of the two red regions did not change but the area of the triangle (Fig 5) grew, the whole area between the new curve SPT and the line ST has increased. This shows that unless the curve is a semicircle we can always increase the area in question by moving points S and T. This proves Lemma 2 and with it Statement 1.
Elegant as it is this proof of Statement 1 contains a flaw. On each of the three steps we
assumed that the shape answering conclusions of the steps existed and the
Lemmas have only been proved under this assumption. Ultimately, we assumed that there exists a figure having a maximum area
among all the shapes with the same perimeter. Under this assumption we proved that such a shape
is bound to be a circle. Denote the existence hypothesis as H. What we have actually shown is an implication
Existence of the optimal shape in the sense of Statement 1 is not at all obvious. For example, if Statement 1 required us to determine a shape with the smallest area for a given perimeter, such shape would not exist at all. Once we understood this point it's less important to actually complete the proof. H is proven with a limiting procedure which is quite simple but requires some basic elements of Calculus.
Both Statements 1 and 2 can be expressed in a more algebraic form which indeed underlines the fact that they are equivalent. Denote the perimeter and area of a planar shape L and A, respectively. Then
4πA ≤ L²,
which is known as the Isoperimetric Inequality. The equality only holds for a circle. Fixing L we get Statement 1. Fixing A Statement 2. Isoperimetric Inequality can be generalized in several ways. For one, it extends into higher dimensional spaces. For example, if S is a surface area while V a volume of a 3d body then
36πV² ≤ S³.
The inequality translates into two equivalent statements of which one claims that among all three dimensional solid bodies with a given surface area the sphere has the largest volume. What is the other one?
Another generalization pertains to the Geometric Theory of Fuzzy Sets. Regular sets for which it's assumed to be known whether a point belongs to a set or not are called crisp among the fuzzy sets. For a fuzzy set a point may belong to a set with a certain degree that changes from 0 (does not belong at all) to 1 (belongs unequivocally). The theory defines fuzzy circles and fuzzy spheres. In Reference [1] I have shown that the general Isoperimetric Inequality holds for fuzzy sets. The equality is only reached for crisp circles, spheres and their multidimensional analogues.
Pappus of Alexandria (ca 300 A.D.) wrote
Bees, then, know just this fact which is useful to them, that the hexagon is greater than the square and the triangle and will hold more honey for the same expenditure of material in constructing each. But we, claiming a greater share of wisdom than the bees, will investigate a somewhat wider problem, namely that, of all equilateral and equiangular plane figures having the same perimeter, that which has the greater number of angles is always greater, and the greatest of them all is the circle having its perimeter equal to them.
In a sense it is very satisfying to have the circle as a solution to Statement 1. The circle is unique in its roundness. It's symmetric in every straight line passing through its center. The circle is perfect and, thus, is a good candidate to satisfy the Isoperimetric Theorem. Polygons are less smooth than a circle, less perfect one can say. Still in every family of polygons there is one which is less imperfect than the rest. Interestingly, in their respective families these "less imperfect shapes" satisfy isoperimetric conditions.
- Among all triangles with the same perimeter, the equilateral one has the largest area
- Among all quadrilaterals with the same perimeter, the square has the largest area
- In particular, among all rectangles with the same perimeter, the square has the largest area
- This latter fact is equivalent to √ab ≤ (a + b)/2, a particular case of the inequality between the geometric an arithmetic means.
- ...
- Among any finite number of regular polygons with the same perimeter, the one with the largest number of sides has the largest area.
- Among all n-gons (n fixed) with the same perimeter the regular one has the largest area. (This is known as Zenodorus Theorem, see [Tikhomirov, pp 11-15].
- Each of the statements above has an equivalent where the area is given.
- As in Lemma 2, among all plane curves of fixed length with fixed endpoints, a circular arc encloses a maximum area between it and the line joining its endpoints.
- Of all polygons with n sides inscribed in a given circle, the regular one has the largest area.
References
- A. Bogomolny, On the Perimeter and Area of Fuzzy Sets, International Journal of Fuzzy Sets and Systems, 23(1987), 257-269.
- R. Courant and H.Robbins, What is Mathematics?, Oxford University Press, NY, 1996.
- W. Dunham, The Mathematical Universe, John Wiley & Sons, 1994
- R. Honsberger, Ingenuity in Mathematics, MAA, New Math Library, 1970
- D. A. Kryjanovsky, Isoperimetry, Fizmatgiz, Moscow, 1959 (in Russian)
- P. J. Nahin, When Least Is Best, Princeton University Press, 2007 (Fifth printing).
- J. A. Paulos, Beyond Numeracy, Vintage Books, 1992
- H. Rademacher and O. Toeplitz, The Enjoyment of Mathematics, Dover Publications, 1990.
- V. M. Tikhomirov, Stories about Maxima and Minima, AMS-MAA, 1990
|Contact| |Front page| |Contents| |Did you know?| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579962
