Daniel Dan's Optimization in Three Variables
Problem
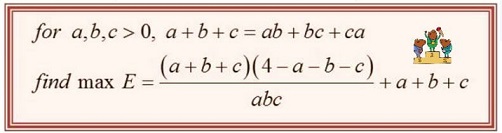
Solution
Set $p=a+b+c\,$ $q=ab+bc+ca\,$ and $r=abc.\,$ The constraint reads $p=q,\;$ but $p^2\ge 3q,\,$ implying $p^2\ge 3p,\,$ or, $p\ge 3.\,$ On the other hand, $p^2\ge 3pr,\,$ so that $\displaystyle r\le\frac{p}{3}.$
If $p=4,\,$ then
$\displaystyle\begin{align} E-4 &= \frac{p(4-p)}{r}+p-4=(4-p)\left(\frac{p}{r}-1\right)\\ &\le 0, \end{align}$
so that $E\le 4.\,$ In fact, $\max E=4,\,$ for $p=4.\,$ The maximum is attained for $(a,b,c)=\displaystyle\left(\frac{2}{3},\frac{2}{3},\frac{8}{3}\right)\,$ and permutations.
If $3\le p\le 4,\,$ It follows from Schur's inequality that $p^4-5p^2q+4q^2+6pr\ge 0,\,$ and, since $p=q,\,$ $r\ge\displaystyle\frac{(4-p)(p-1)p}{6}\,$ and, subsequently, $E-6=\displaystyle\frac{(p-4)(p-3)}{p-1}\le 0.\,$ so that, in this case, $\max E=6\,$ which is attained for $p=3,\,$ with $(a,b,c)=(1,1,1).$
Acknowledgment
As I understand, the story is somewhat convoluted. Daniel Dan has kindly posted the problem at the CutTheKnotMath facebook page and simultaneously at the Imad Zak facebook group. At the CutTheknotMath facebook page, Leo Giugiuc left a comment: "Difficult and beautiful. But who knows? Maybe there are some of the new solvers who solve it in one row. Because my solution is difficult and requires broad knowledge." A day later, Imad Zak posted his solution (above) and mentioned my page in the comment which I interpret as a silent invitation to reproduce his proof at my site, which I do. My sincerest thank to everyone involved. Leo was right - the solution is far from simple and requires much ingenuity and a good deal of knowledge. Kudos to Imad Zak.

![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73586315
