Three Random Points on a Circle
What Is This About?
Problem

Solution 1
We shall reformulate the problem and then exploit an Semicircle Coveragealready solved one.
For three uniformly random points on a circle the following two questions are equivalent:
The semicircles of which the three points are the centers cover the circle.
The triangle with vertices at the three points has the center of the circle in its interior.
The problems are equivalent. Indeed, consider a borderline case where two of the points are collinear with the center of the circle. Denote the points $A,$ $B,$ $C$ and the center of the circle $O.$ And assume that, say, $AC$ is a diameter of the circle.

Point $B$ is on one of the semicircles defined by $AC.$ Let $D$ be the midpoint of the semicircle define by $AC$ that does not contain $B.$ Then $D$ is outside the semicircle defined by $B.$ Shifting $A$ and/or $C$ towards $B$ will leave $D$ exposed, not covered by any of the three semicircles. Simultaneously, the center $O$ will drop out of $\Delta ABC.$
Now, with a reference to a problem of covering a circle with three semicircles, the probability of having $O$ in the interior of $\Delta ABC$ equals $\displaystyle \frac{1}{4}.$
Solution 2
The center $O$ is inside $\Delta ABC$ iff that is an acute triangle which means that all three central angles $AOB,$ $BOC,$ $COA$ are less than $180^{\circ}.$ It follows that their semicircles intersect pairwise and thus cover the whole of the circle.

Now, with a reference to a problem of Semicircle Coveragecovering a circle with three semicircles, the probability of having $O$ in the interior of $\Delta ABC$ equals $\displaystyle \frac{1}{4}.$
Solution 3
Let us say that $O$ is the first point we generate. This will be our point of reference. From this point, we will use polar coordinate system (counterclockwise) to determine the position of $A$ (our second point, with $\widehat{OCA}=\alpha$) and then the position of $B$ (our third point, with $\widehat{OCB}=\beta$). Let $C$ be the center of the circle.
Let us call $\check{A}$ and $\check{B}$ the two random variables (uniforms on $[0,2\pi]$). Let us distinguish between two cases (there are two letters $B$ in each graph for the two "extreme" letters $B):$
- If $0<\alpha\leq\pi$ then the $\beta$ that allow $C$ to be in the triangle are those in $[\pi,\pi+\alpha]$.
- If $\pi<\alpha\leq2\pi$ then the $\beta$ that allow $C$ to be in the triangle are those in $[\alpha-\pi,\pi]$.
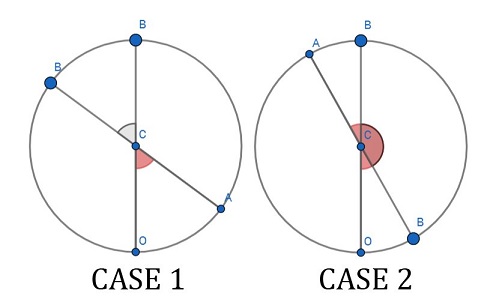
The probability $p$ that $C$ is inside the triangle $OAB$ is (with convenient notations for probability density functions):
$\displaystyle \begin{align} p & = \int_{0}^{\pi}\mathbb{P}(\check{B}\in[\pi,\pi+\alpha]|\check{A}=\alpha)\mathbb{P}(\check{A}=\alpha)d\alpha\\ &\qquad\qquad\qquad+\int_{\pi}^{2\pi}\mathbb{P}(\check{B}\in[\alpha-\pi,\pi]|\check{A}=\alpha)\mathbb{P}(\check{A}=\alpha)d\alpha \\ & = \int_{0}^{\pi}\Big(\frac{\pi+\alpha-\pi}{2\pi}\Big)\Big(\frac{1}{2\pi}\Big)d\alpha+\int_{\pi}^{2\pi}\Big(\frac{\pi-(\alpha-\pi)}{2\pi}\Big)\Big(\frac{1}{2\pi}\Big)d\alpha \\ & = \int_{0}^{\pi}\Big(\frac{\alpha}{2\pi}\Big)\Big(\frac{1}{2\pi}\Big)d\alpha+\int_{\pi}^{2\pi}\Big(\frac{2\pi-\alpha}{2\pi}\Big)\Big(\frac{1}{2\pi}\Big)d\alpha \\ & = \int_{0}^{\pi}\Big(\frac{\alpha}{2\pi}\Big)\Big(\frac{1}{2\pi}\Big)d\alpha+\int_{\pi}^{0}\Big(\frac{\delta}{2\pi}\Big)\Big(\frac{1}{2\pi}\Big)(-1)d\delta \\ & = \int_{0}^{\pi}\Big(\frac{\alpha}{2\pi}\Big)\Big(\frac{1}{2\pi}\Big)d\alpha+\int_{0}^{\pi}\Big(\frac{\delta}{2\pi}\Big)\Big(\frac{1}{2\pi}\Big)d\delta \\ & = 2\int_{0}^{\pi}\Big(\frac{\alpha}{2\pi}\Big)\Big(\frac{1}{2\pi}\Big)d\alpha \\ & = \frac{1}{4} \end{align}$
(where we used the change of variable $\delta=2\pi-\alpha$)
Acknowledgment
This is a simplified (2D) version of problem A-6 from the 1992 Putnam Competition that was brought to my attention by Mike Lawler, for which I am sincerely grateful. Solution 3 is by Achraf.
- What Is Probability?
- Intuitive Probability
- Probability Problems
- Sample Spaces and Random Variables
- Probabilities
- Conditional Probability
- Dependent and Independent Events
- Algebra of Random Variables
- Expectation
- Probability Generating Functions
- Probability of Two Integers Being Coprime
- Random Walks
- Probabilistic Method
- Probability Paradoxes
- Symmetry Principle in Probability
- Non-transitive Dice
![]()
|Contact| |Front page| |Contents| |Probability|
Copyright © 1996-2018 Alexander Bogomolny73571802
