A Property of Perspective Triangles
What is this about?
Problem
Let $ABC$ and $A'B'C'$ be two perspective triangles so that $AA',$ $BB',$ $CC'$ meet at a point $P.$ Define $Y=AC'\cap A'C$ and $Z=AB'\cap A'B.$
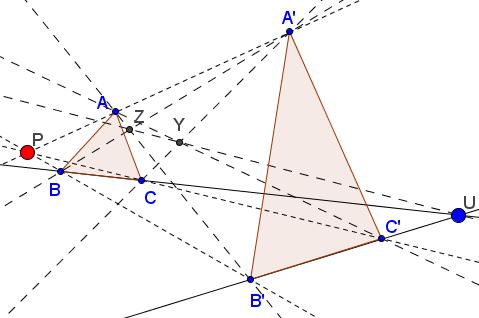
Then $BB',$ $CC',$ and $YZ$ concur at a point $(U$ in the diagram.)
Proof
Letting $PAA'$ be the line at infinity, the problem reduces to a simple one:
Let $UBB'$ be a triangle. A line parallel to $BB'$ intersects $BU$ and $B'U$ at $C$ and $C',$ respectively. Two parallel lines from $B$ and $C$ intersect another pair of parallel lines through $B'$ and $C'$ at $Y$ and $Z.$ Show that the line $YZ$ passes through $U.$
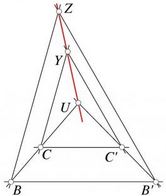
The main tool for the solution is Thales' theorem and its inverse.
Assume the line through $C$ meets $UZ$ at $Y_1$ and that through $C'$ meets $UZ$ ay $Y_2.$ Then we have the following proportions:
$\displaystyle\frac{Y_{1}Z}{UY_{1}}=\frac{BC}{CU}=\frac{B'C'}{C'U}=\frac{Y_{2}Z}{UY_{2}}.$
Assuming the length of $UZ=1,$ that of $UY_{1}=t$ and $UY_{2}=s,$ the above reduces to $\displaystyle\frac{1-t}{t}=\frac{1-s}{s}$ from which $t=s$ and, consequently, also $Y_{1}=Y_{2}.$
Acknowledgment
The problem (which generalizes one part of a previously posted problem) and its solution are due to Francisco Javier García Capitán (Spain).
Machú Búnis noticed that the statement is directly the Desargues theorem applied to triangles $A'BC$ and $AB'C'$ triangles. It follows that the above derivation can be used to proving the latter.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73574474
