Surprise: Right Angle in Circle
What Is This About?
Source
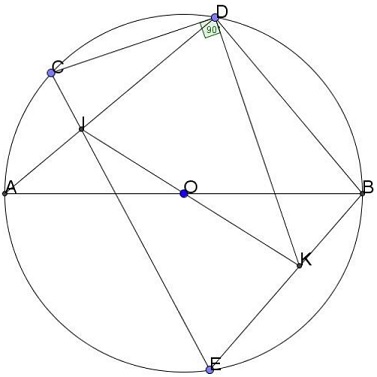
(There is a small detail in this diagram that may, if not give away, then, at least, suggest the origin of the problem - and its solution.)
Problem
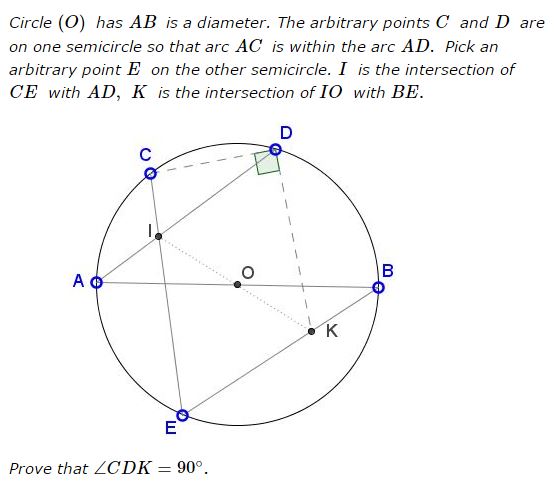
Proof
Forget, for a moment, of the manner in which point $K\;$ has been defined. Let $CF\;$ be a diameter of circle $(O)\;$ and consider the inscribed hexagon $ABECFD.\;$
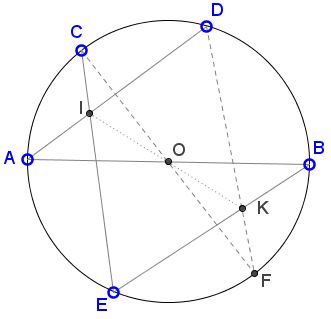
According to Pascal's theorem, in hexagon $ABECFD,\;$ inscribed into circle $(O),\;$ the intersections of the three pairs of opposite side lines are collinear. These are $I=AD\cap CE,\;$ $O=AB\cap CF,\;$ and, say, $K'=DF\cap BE,\;$ are collinear. In other words, $K'=IO\cap BE,\;$ making $K'=K.$
Now, since inscribed angle $CDF\;$ is subtended by diameter $CF,\;$ it is right: $\angle CDK=90^{\circ}.$
Acknowledgment
The problem has been posted to the Imad Zak Math facebook group by Charybdis Mellery, with a reference to a Vietnamese friend of his.
Now, I feel this problem is an excellent example of the process of mathematical discovery - by looking back at a known fact, playing with it, changing the view point. I believe this is how he author of the problem came up with it. What I think gives this away is the presence of segment $BD\;$ in the source diagram, the segment that is absolutely irrelevant to the problem, but may suggest that the points on the circle may relate to each other in ways other than that stated in the problem. Pascal's theorem then comes to mind and the missing sixth point is easily conjured up.
Symmedian
- All about Symmedians
- Symmedian and Antiparallel
- Symmedian and 2 Antiparallels
- Symmedian in a Right Triangle
- Nobbs' Points and Gergonne Line
- Three Tangents Theorem
- A Tangent in Concurrency
- Symmedian and the Tangents
- Ceva's Theorem
- Bride's Chair
- Star of David
- Concyclic Circumcenters: A Dynamic View
- Concyclic Circumcenters: A Sequel
- Steiner's Ratio Theorem
- Symmedian via Squares and a Circle
- Symmedian via Parallel Transversal and Two Circles
- Symmedian and the Simson
- Characterization of the Symmedian Point with Medians and Orthic Triangle
- A Special Triangle with a Line Through the Lemoine Point
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73571166
