Inscribed Angles: What is this about?
A Mathematical Droodle

---

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

---

Buy this applet What if applet does not run?

A few words

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2015 Alexander Bogomolny

Inscribed Angles

Two angles inscribed in a circle, if they subtend the same arc, and are thus associated with the same central angle. The two are therefore equal.

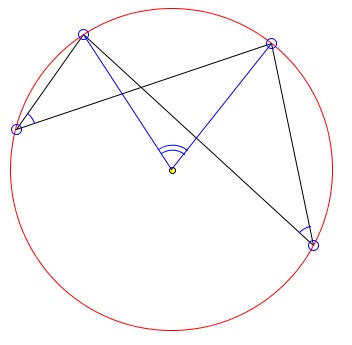
(This is Proposition III.21 form Euclid's Elements.)

In fact, the opposite is also true: if ∠CAD = ∠CBD and the angles are "similarly oriented", then the four points A, B, C and D are concyclic.

Two angles may or may not have the same orientation. The idea of angle's orientation is captured in the notion of directed angles:

Definition

The directed angle (AC, AD) is the angle through which the ray AC should be rotated in the positive (counterclockwise) direction in order to coincide with AD.

The definition simply propagates the idea of orientation of a line (positive/negative direction on a line) and that of a plane (positive/negative rotation of a plane) to that of angle.

We may reformulate the above statement: four non-collinear points A, B, C, D are concyclic iff (AC, AD) = (BC, BD).

Given two (oriented lines) l and l', we may, by selecting points on the lines, define the directed angle (l, l'). The notation is concise and helpful. For example, it allows a simple formulation of the following property:

(l, l'') = (l, l') + (l', l'').

Quite often we wish to consider straight lines instead of rays. It is common then to work with directed angles modulo 180°.

Angles in Circle

1. Angle Subtended by a Diameter
2. Inscribed Angles
3. Inscribed and Central Angles in a Circle
4. Munching on Inscribed Angles
5. Sangaku with Angle between a Tangent and a Chord
6. Secant Angles in a Circle
7. Secant Angles in a Circle II
8. Thales' theorem

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2015 Alexander Bogomolny