Regular Hexagon from Arbitrary Triangle
What Might This Be About?
Problem
$G$ is the centroid of $\Delta ABC.$ $k\ne 0$ a real number. Construct $A',$ $B',$ $C'$ and $A'',$ $B'',$ $C''$ as homothetic images of $A,$ $B,$ $C$ in $G$ with coefficients $k$ and $-k,$ respectively. Equilateral triangles $A'B''B_A,$ $B''C'B_C,$ $C'A''A_C,$ $A''B'A+B,$ $B'C''C_B,$ $C''A'C_A$ are constructed either all internally or all externally to the hexagon $A'B''C'A''B'C''.$
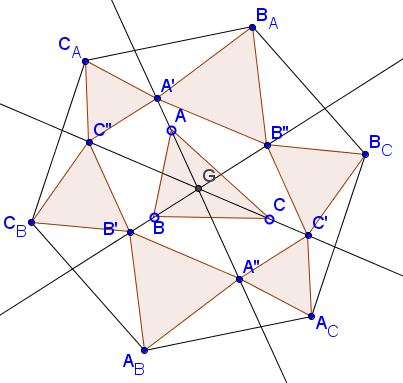
Prove that $A_BA_CB_CB_AC_AC_B$ is a regular hexagon.
Proof
It is easy to show that $A'B''C'A''B'C''$ is a parahexagon.
For an equilateral triangle $ABC,$ $A'B''C'A''B'C''$ is regular. An affine transformation of $\Delta ABC$ applies also to $A'B''C'A''B'C''$. Since any triangle is an affine transformation of an equilateral one, $A'B''C'A''B'C''$ is an affine-regular hexagom.
The assertion is then just a direct consequence of the Napoleon-Barlotti Theorem.
Acknowledgment
The problem has been posted at the CutTheKnotMath facebook page by Trinh Xuan Minh.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73569754
