Construction of Parahexagon
What is it?
A Mathematical Droodle

---

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

---

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

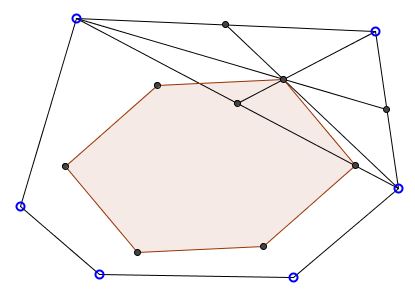
Parahexagon is a hexagon whose opposite sides are parallel and equal. This is an analogue of parallelogram, but with 6 sides. The term I believe has been coined by Kasner and Newman in their Mathematics and the Imagination. (Eves designates the polygons parpolygons.) The applet attempts to demonstrate the following construction of a parahexagon.

Start with any hexagon. Each triple of consecutive vertices forms a triangle. The centers of the successive triangles necessarily form a parahexagon.

Indeed, let the vertices of the given hexagon be denoted as P₁, P₂, P₃, P₄, P₅, and P₆. Consider the centers of two consecutive triangles described above, say, P₁P₂P₃ and P₂P₃P₄. The triangles share a side, viz., P₂P₃. Denote its midpoint as M. In ΔP₁P₂P₃, the center lies on the median P₁M and divides it in the ratio 2:1 counting from P₁. Similarly, in ΔP₂P₃P₄, the center lies on the median P₄M and divides it in the ratio 2:1 counting from P₄. It follows, that in ΔP₁MP₄, the line joining the two centers is parallel to P₁P₄ and is equal 1/3 of the latter.

The opposite side of the hexagon under investigation joins the centers of triangles P₄P₅P₆ and P₅P₆P₁. It, too, is parallel to P₁P₄ and equals its third.

That result admits a generalization that also covers the Varignon parallelogram.

Polygons with opposite sides parallel but not necessarily equal still have interesting properties.

References

1. H. Eves, A Survey of Geometry, Allyn and Bacon, 1972
2. E. Kasner and J. Newman in their Mathematics and the Imagination, Dover Publications (March 28, 2001)

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|