The SSS
The acronym SSS (side-side-side) refers to the criterion of congruence of two triangles: if the three sides of one equal the three sides of the other, the two triangles are congruent. In Euclid's Elements the formulation is somewhat different. Elements I.8 reads, If two triangles have the two sides equal to two sides respectively, and have also the base equal to the base, they will also have the angles equal which are contained by the equal straight lines. The reason for a strange, asymmetric formulation is that Elements I.4 is about what is known nowadays as SAS and establishes the congruence of two triangles by a pair of equal sides and the angle they include. As you'll see shortly, Euclid has based his proof of SSS on that of SAS. Further, in Elements I.4, Euclid indeed concludes that under the SAS conditions, the remaining side and the remaining two angles in one triangle equal their counterparts in the other. He did not find it necessary to mention that fact in a later proposition. But he took care to make the two formulations sound alike so as to draw attention to the relationship between the two that he built and exploited.
On this page I have collected a few proofs of the SSS criterion from several popular geometry texts. Let's start with Euclid's proof.
Proof 1 (Euclid)
Let ABC, DEF be two triangles having the two sides AB, AC equal to the two sides DE, DF respectively, namely AB to DE, and AC to DF; and let them have the base BC equal to the base EF.
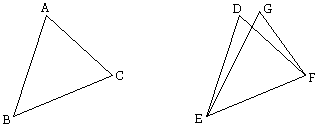
I say that the angle BAC is also equal to the angle EDF.
For, if the triangle ABC be applied to the triangle DEF, and if the point B be placed on the point E and the straight line BC on EF, the point C will also coincide with F, because BC is equal to EF.
Then, BC coinciding with EF, (so that) BA, AC wiil also coincide with ED, DF; for, if the base BC coincides with the base EF, and the sides BA, AC do not coincide with ED, DF but fall beside them as EG, GF, then given two straight lines constructed on a straight line (from its extremities) and meeting in a point, there will have been constructed on the same straight line (from its extremities), and on the same side of it, two other straight lines meeting in another point and equal to the former two respectively, namely each to that which has the same end with it.
But they cannot be so constructed I.7
Therefore it is not possible that, if the base BC be applied to the base EF, the sides BA, AC should not coincide with ED, DF; they will therefore coincide, so that the angle BAC will also coincide with the angle EDF, and be equal to it. Q.E.D.
![]()
Sir Thomas Heath's commentary to Euclid contains a proof by the Hellenized Jewish philosopher Philo of Alexandria (or Philo Judeaus) that he plucked from Proclus' Commentary on the first book of Euclid. Sir Thomas comments: This alternative proof avoids the use of I.7, and it is elegant; but it is inconvenient in one respect, since three cases have to be distinguished. Proclus gives the proof in the following order.
Proof 2 (Philo Judeaus)
Let ABC, DEF be two triangles having the two sides AB, AC equal to the two sides DE, DF respectively, namely AB to DE, and AC to DF; and let them have the base BC equal to the base EF.
Let the triangle ABC be applied to the triangle DEF, so that B is placed on E and BC on EF, but so that A falls on the opposite side EF from D, taking position G. Then C will coincide with F, since BC is equal to EF.
Now FG will either be in a straight line with DF, or make an angle with it, and in the latter case the angle will either be interior to the figure or exterior.
Let FG be in a straight line with DF.

Then, since DE is equal to EG, and DFG is a straight line, DEG is an isosceles triangle, and the angle at D is equal to the angle at G [I.5].
Let DF, FG form an angle interior of the figure.
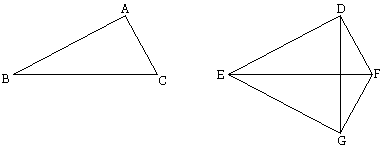
Let DG be joined. Then, since DE, EG are equal, the angle EDG is equal to the angle EGD. Again, since DF is equal to FG, the angle FDG is equal to the angle FGD.
Therefore, by addition, the whole angle EDF is equal to the whole angle EGF.
Let DF, FG form an angle exterior ot the figure.

Let DG be joined. The proof proceeds as in the last case, except that subtraction takes place of addition, and the remaining angle EDF is equal to the remaining angle EGF.
Therefore in all three cases the angle EDF is equal to the angle EGF, that is, to the angle BAC.
(Heath makes the following observation: It will be observed that, in accordance with the practice of the Greek geometers in not recognizing as an angle any angle not less than two right angles, the re-entrant angle of the quadrilateral DEFG is ignored and the angle DFG is said to be outside the figure.)
![]()
A proof that combines I.8 and, in a sense, I.7 is given in the famous text by J. Hadamard.
Proof 3 (J. Hadamard)
Two triangles are equal if they have three respectively equal sides.
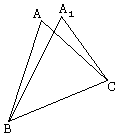
Let there be two triangle ABC and A'B'C', whose sides are respectively equal. Let's place the second triangle so as to make side B'C' coincide with BC and have both triangles lie on the same side of BC. Let BCA1 be the new position of triangle B'C'A'. I claim that point A1 coincides with point A. It would have been evident had line B'A' had the direction of BA or line C'A' the direction of CA. Had it not been so, we would have had two isosceles triangles BAA1 and CAA1, and the perpendicular bisector of AA1 would have to pass through points B and C; in other words, the perpendicular bisector of AA1 would have to coincide with the line BC. But this is impossible, since points A and A1 lie on the same side of BC, and therefore BC can't pass through the midpoint of AA1. The points A and A1 can't therefore be different. The two triangles are bound to be equal.
![]()
We now move to a proof from one of the best modern high school geometry texts -- Geometry: Seeing, Doing, Understanding by H. Jacobs.
The SSS Theorem
If the three sides of one triangle are equal to the three sides of another triangle, the triangles are congruent.
Our proof, after that of Euclid, is based on copying one of the triangles and then showing that the other triangle is congruent to this copy. The figures illustrate the construction and proof.
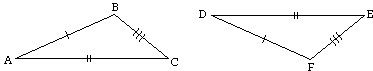
Given: AB = DF, BC = FE, and AC = DF.
Prove: ΔABC ![]() ΔDFE.
ΔDFE.
Proof 4 (H. Jacobs)
The first part: Drawing a new triangle congruent to ΔDEF.
First draw ray AX from point A so that ∠CAX = ∠D (Protractor Postulate). Next choose point P on ray AX so that AP = DF (Ruler Postulate). Draw CP (two points determine a line). ΔAPC ![]() ΔDFE (SAS).
ΔDFE (SAS).

The second part: Showing that the new triangle is congruent to ΔABC.
Draw BP. AP = DF (corresponding parts of congruent triangles are equal) and

Also, PC = FE (corresponding parts of congruent triangles are equal) and

Because ∠1 = ∠2 and ∠3 = ∠4,
The proof is long but the theorem is easy to use. You should learn the SSS Theorem well enough to be able to recall it as a sentence whenever you see it referred to as SSS.
![]()
One more example comes from a venerable elder of geometry textbooks - Kiselev's Geometry - that was first published in 1892.
Proof 5 (Kiselev)
Let ABC and A'B'C' be two triangles such that
It is required to prove that these triangles are congruent. Proving this test by superimposing, the same way as we proved the first two tests, turns out to be awkward, because knowing nothing about the measure of the angles, we would not be able to conclude from coincidence of two corresponding sides that the other sides coincides as well. Instead of superimposing, let us apply juxtaposing.
Juxtapose ΔABC and ΔA'B'C' I such a way that their congruent sides AC and A'C' would coincide (i.e. A would merge with A' and C with C'), and the vertices B and B' would lie on the opposite sides of A'C'. Then ΔABC will occupy the position ΔA'B''C':
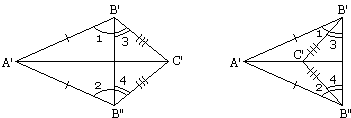
Joining the vertices B' and B'' we obtain two isosceles triangles B'A'B'' and B'C'B'' with the common base B'B''. But in an isosceles triangle, the angles at the base are congruent. Therefore
Now comes the punch line: some of the above proofs are incorrect. Which ones?
References
- J. Hadamard, Leçons de géométrie élémentaire, tome I, 13e édition, 1947, Editions Jacques Gabay, 1988, ISBN 2-87647-038-1.
- T. L. Heath, Euclid: The Thirteen Books of The Elements, v. 1, Dover, 1956
- H. R. Jacobs, Geometry, 3rd edition, W. H. Freeman and Company, 2003
- Kiselev's Geometry. Book I. PLANIMETRY, adapted from Russian by Alexander Givental, Sumizdat, 2006.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander BogomolnyDiscussion
Of the five proofs presented above, which ones are correct and which ones are not? I realize that, coming from different sources, the proofs differ in notations and, although slightly, in terminology. Also, we know little about the treatment the source books afforded to the underlying axioms, lemmas, or theorems. In one case at least -- that is of Euclid's itself -- we know that the proof of the fundamental I.7 is lacking. As a matter of fact it can be patched by considering additional configurations. We should admit nonetheless that, as it now stands, Euclid's treatment is clearly lacking.
Philo's treatment in this sense appears exhaustive: all three possible cases have been observed and followed up. However, the proof still conceals a subtle error of the sort that was discovered in Euclid's treatment of the Exterior Angle Theorem. Explicitly, up to the point of joining D and G the construction could have been performed on a sphere. And that's where the trouble lies. On a sphere, points B' and B'' might not be distinct at all: they may coincide; this would entirely break Philo's argument. If they coincide, there will be two distinct straight lines that meet twice, which is impossible in the Euclidean geometry. Thus assuming B' and B'' distinct presupposes the Eulidean environement.
Hadamard's treatment is the only one that goes through without a hitch (assuming of course that isosceles triangles have been fairly treated previously).
Both Jacobs and Kiselev base their treatment on Philo's and therefore inherit its weakness. In addition, Kiselev omits from consideration one case while Jacobs omits two (and this is out of 3.)
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73531546
