Triangle of Minimum Perimeter
Problem
Given an angle with vertex $O$ and point $P$ within.
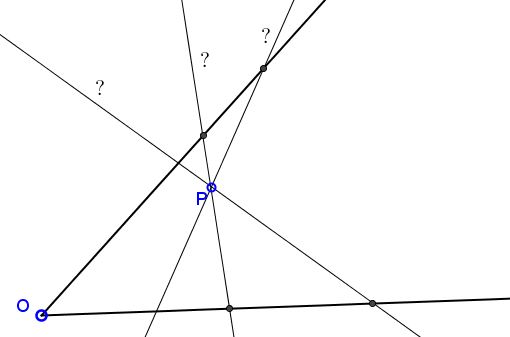
Pass a straight line line through $P$ that cuts off the angle a triangle of least perimeter.
I found this problem in Murray Klamkin's chapter in a book published on the occasion of Howard Eves' eightieth birthday. Up to a point, I follow Klamkin's proof, show that it is somewhat incomplete, and fix the omission.
References
- M. S. Klamkin, Mathematical Creativity in Problem Solving II, in In Eves' Circles, J. M. Anthony (ed.), MAA, 1994
A Lucky Observation
Klamkin writes that he "came across that problem when in high school and it took him about two weeks working off and on before he solved it. The difficulty with this problem was in that the key geometric theorem that unlocked the solution was unexpected." Much later when he was in charge of writing a programmed text in geometry, he managed to figure out some motivation for the solution, viz., that in solving extrema problems it is often very useful to consider level curves.
This was based on another important observation: all tangents to a circle inscribed in a given angle cut off triangles of the same perimeter:

(So we relax the problem and consider straight lines that do not necessarily pass through $P!$)
If $B'$ and $C'$ are the points of tangency of the circle with the legs of the angle, then the perimeter of any cutoff triangle equals $OB'+OC'$ which is the same for all tangents to the circle. It follows that the circular arcs inscribed in the angle are the level curves of function $f(\Delta)$ on the set $\{\Delta\}$ of cutoff triangles $\Delta$ that assigns to every triangle its perimeter.
This leads to a construction.
Construction
We need to construct a circle through point $P$ tangent to the legs of the angle, and then a tangent to that circle at $P.$
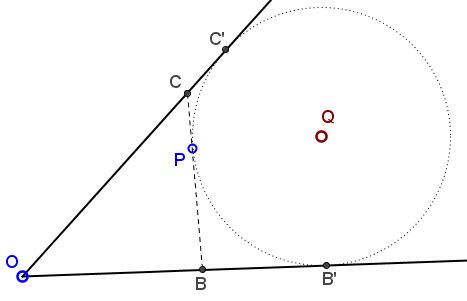
The second part is easy (just draw a line perpendicular to the radius of the circle at $P).$ The first part is just a special case of the problem of Apollonius. (To remind, the problem of Apollonius is two construct a circle tangent to the given three circles. Ours is a degenerate case where two circles straighten into lines and one shrinks into a point.) This Apollonius circle appears in several related constructions, and this is why I think that "The lucky observation" that led young Klamkin to the solution, became in time a useful tool to his adult self.
Looking back
So we solved the problem. Now, following George Polya's advice, let's have a look back. Is everything OK? Have I missed anything? Indeed, I have!
The fact is that the problem of Apollonius used here as an auxiliary step has two solutions, not a unique one:
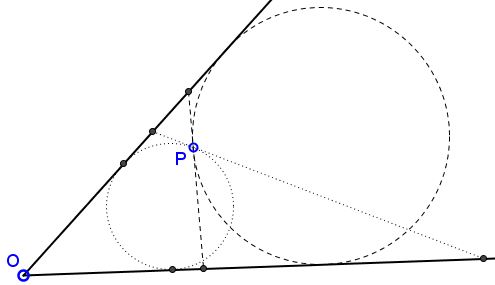
Which one should we choose as a means to solving the problem at hand?
To resolve this question, think of every circle inscribed into an angle as consisting of two arcs defined by the tangency points. Let's call them, say, inner (for the arc nearer the vertex $O$) and outer (the farther away from the vertex.) I claim that the circle for which the line through $P$ is tangent to the inner arc is the solution, unless $P$ lies on the angle bisector (in which case the two Apollonian circles share the tangent through $P.)$
Here is why.
Mopping up
Consider the two Apollonian circles through $P$ and their tangents perpendicular to the angle bisector - the inner for the big circle, the outer for the small one. The latter has clearly bigger area and perimeter. For the former, as we know, the tangent through $P$ will cut a triangle of exactly same perimeter.
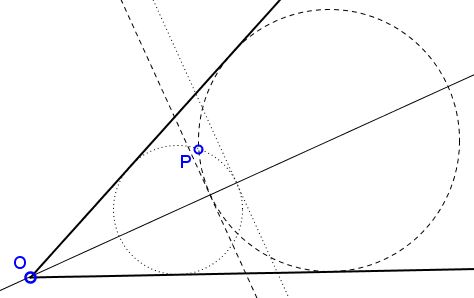
For the latter, the perimeter grows as the tangents moves away from being perpendicular to the angle bisector. By transitivity, the cutoff triangle generated by the tangent to an inner arc will always have perimeter less than the one formed by a tangent to an outer arc.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579844
