Trisect Segment: 2 Circles, 4 Lines

Proof

Observe that, by the construction, in the diagram below, $P$ is the midpoint of $CG$ while $E$ is the midpoint of $AG.$ It thus follows that $F$ is the centroid in $\Delta ACG,$ implying $AF:FP=2:1,$ but $P$ is also the midpoint of $AB.$ We therefore get the sequence of ratios: $AP:AF=3:2,$ $AB:AF=6:2=3:1.$

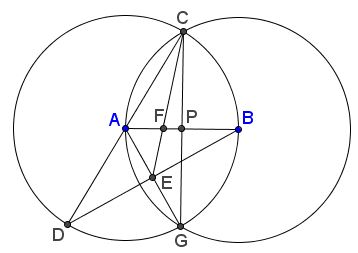
In the article referred to below a similar (but even shorter) argument was applied to $\Delta BCD,$ with $CE$ and $AB$ as the medians.

References

1. R. Styer, Trisecting a Line Segment (With World Record Efficiency!)

Related material Read more...
	Various Geometric Constructions
	How to Construct Tangents from a Point to a Circle
	How to Construct a Radical Axis
	Constructions Related To An Inaccessible Point
	Inscribing a regular pentagon in a circle - and proving it
	The Many Ways to Construct a Triangle and additional triangle facts
	Easy Construction of Bicentric Quadrilateral
	Easy Construction of Bicentric Quadrilateral II
	Star Construction of Shapes of Constant Width
	Four Construction Problems
	Geometric Construction with the Compass Alone
	Construction of n-gon from the midpoints of its sides
	Short Construction of the Geometric Mean
	Construction of a Polygon from Rotations and their Centers
	Squares Inscribed In a Triangle I
	Construction of a Cyclic Quadrilateral
	Circle of Apollonius
	Six Circles with Concurrent Pairwise Radical Axes
	Tangent to Circle in Three Steps
	Regular Pentagon Construction by K. Knop

|Contact| |Front page| |Contents| |Eye opener| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny