Construct a cyclic quadrilateral, given the lengths of its sides in a prescribed order.
Given 4 numbers a, b, c, d which are assumed to be the successive side lengths of a quadrilateral, if one of them is greater than the sum of the remaining three, the construction is rather obviously impossible. There is no quadrilateral whose sides satisfy, say, a > b + c + d. Such cases aside, the construction is always possible.
Construct a cyclic quadrilateral, given the lengths of its sides in a prescribed order.
Assume the desired cyclic quadrilateral exists:
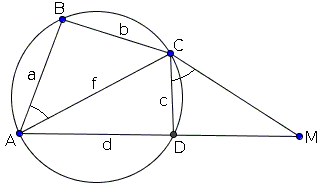
Draw CM, with M on the extension of AD, so that ∠DCM = ∠BAC. This makes triangles ABC and CDM similar because
∠ABC = 180° - ∠ADC = ∠CDM.
The similarity of the triangles implies a proportion DM/b = c/a, so that
DM = bc/a.
Additionally, CM/f = c/a, which tells us that C is located on the locus of point whose distances to points A and M are in a given ratio c/a. The locus is an Apollonian circle.
This information is sufficient to carry out the construction. (In the following C(O, r) will denote the circle with center O and radius r.)
Let d be the largest of the four given lengths.
- Draw AD = d and extend it to M so that DM = bc/a.
- Find C at the intersection of two circles: C(D, c) and the Apollonian circle defined by AC/DM = c/a.
- B is found at the intersection of two circles C(A, a) and C(C, b).
The circle of Apollonius crosses AM at point K such that AK = (ad + bc)/(a + c). (AM = d + bc/a, and this is divided in the ratio c/a.)
K is to the left of or on D exactly when AK ≤ d or, equivalently, b ≤ d. This condition holds by the choice of d as the largest of the four numbers.
If so, KD = d - (ad + bc)/(a + c) = (cd - bc)/(a + c). This is less than c:
(cd - bc)/(a + c) - c = [c/(a + c)](d - b - a - c) < 0.
Thus we can be sure that in the second step the two circles intersect.
In the third step, we simply get two triangles ABC and CDM with proportional sides, so that the two are similar. In particular, ∠ABC = ∠CDM or, which is the same, ∠ABC + ∠ADC = 180°. And so the quadrilateral ABCD is cyclic.
The construction determines the quadrilateral uniquely, however, if we disregard the order of the sides, there are, in principle, 6 different cyclic quadrilaterals with sides a, b, c, and d. All have the same area given by Brahmagupta's formula:
S = √(s - a)(s - b)(s - c)(s - d),
where s is the semiperimeter of the quadrilateral: s = (a + b + c + d)/2.
All six also share the circumcircle which follows from the formula for the circumradius:
16R² = (ad + bc)(ac + bd)(ab + cd) / [(s - a)(s - b)(s - c)(s - d)].
References
- R. A. Johnson, Advanced Euclidean Geometry (Modern Geometry), Dover, 1960, pp. 82-83
