PPL: An Elementary Solution
Below I give an elementary Euclidean construction to a variant of the Problem of Apollonius:
Find a circle through two given points \(A\) and \(B \) and tangent to a given line \(m\):
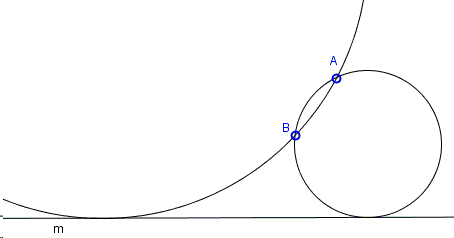
Rather obviously the problem has no solutions if the given line separates the given points (i.e., if the points are on different sides of the line.)
(The applet below illustrates the proof. Points \(A, B\) and line \(m\) are draggable. This permits changing the configuration, but within certain limitations.)
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Construction
Find a circle through two given points \(A\) and \(B \) and tangent to a given line \(m\):

Let's analyze the problem assuming that a solution has been found. There is a circle through \(A\) and \(B\) that touches \(m\) at point \(T:\)
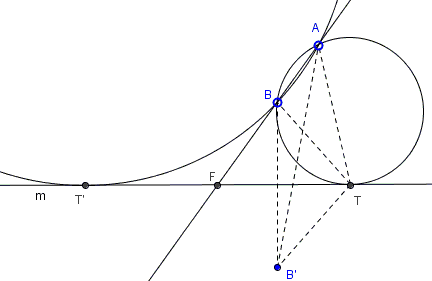
Let \(B'\) be the reflection of \(B\) in \(m\), \(F\) the intersection of \(AB\) with \(m.\) Start chasing the angles:
\( \begin{align} \angle ATB' &= \angle ATB + \angle BTB' \\ &= \angle ATB + \angle BTF + \angle BTF \\ &= \angle ATB + \angle BAT + \angle BTF \\ &= \angle FBT + \angle BTF \\ &= 180^{\circ} - \angle BFT. \end{align} \)
Thus, all it takes to find point \(T\) (and with it solve the problem) is finding a circle with the chord \(AB'\) subtending a certain angle:
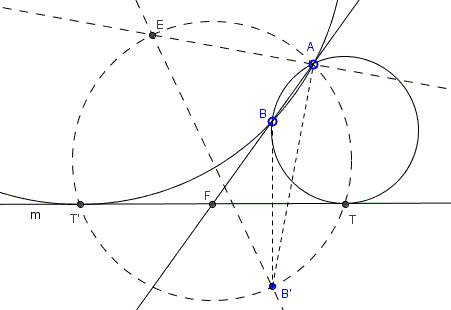
Assuming the problem is solvable, i.e. \(m\) does not separate \(A\) and \(B\), there are, in general, two solutions. But if \(AB\parallel m\), the solution is unique. In case of wo solutions, the tangency points \(T\) and, say, \(T'\) are symmetric with respect to \(F.\)
References
- N. Altshiller-Court, College Geometry, Dover, 1980, #508
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73586069
