Short Construction of the Geometric Mean

The geometric mean of two positive numbers a and b is the (positive) number g whose square equals the product ab:

  g2 = ab.

The geometric mean makes frequent appearances in various geometric situations. One of the simplest arises in a dissection of the golden triangle. The latter configuration admits a generalization. Indeed, if two isosceles triangles OTB and OAT are similar, as in the diagram below, their corresponding sides satisfy the proportion OT/BO = AO/OT, meaning OT is the geometric mean of AO and BO, for any two segments AO and BO.

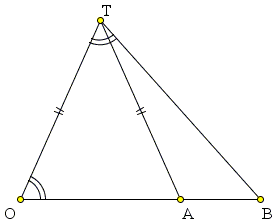
  geometric mean in two similar isosceles triangles

Based on this configuration, C. O. Tuckey suggested in 1929 a short and elegant construction of the geometric mean of two lines segments.

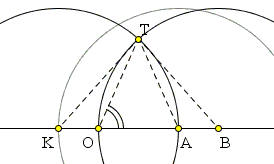
  short construction of geometric mean with two similar isosceles triangles

Assume three points O, A, B are placed on a line, with A and B on the same side relative to O. Tuckey's construction consists of drawing three circles, all with the same radius R = OB:

 
  1. Draw circle C(B, R),
  2. Draw circle C(A, R) and mark its intersection with the line OAB across O as K,
  3. Draw circle C(K, R) and let T be one of the intersections of C(K, R) and C(B, R).

Then OT = √AO·BO.


Indeed, BT = BO as two radii of the same circle C(B, R), and OT = AT, by the symmetry of the construction (AB = KO), which places the resulting configuration into the aforementioned framework of two similar isosceles triangles.

The background for the 1929 article and the construction is Lemoine's idea expressed in his Géométrographie for assessing the simplicity of the construction by the total number of elementary operations (setting one tip of a compass or a straightedge to a point or to a line, drawing a circle or a line). According to D. E. Smith, Lemoine considered La Géométrographie his greatest work, although he got more credit for his part in the rebirth of triangle geometry at the end of the 19th century. The notion that the size of a derivation or construction may play an important role in mathematics did not appear to attract mathematicians until relatively recently, with the emergence of the Complexity Theory, see, for example, O. Goldreich's chapters in Mathematics Unlimited - 2001 and Beyond or Princeton Companion to Mathematics.

C. O. Tuckey ends his paper with a veiled challenge. "If a construction of less complexity has been devised, I hope some reader of the Mathematical Gazette will supply it." Truth be told, I am unaware whether anybody picked up the gauntlet in the 80 years since. I am still charmed by the elegance of the construction.

References

  1. O. Goldreich, Computational Complexity, in Mathematics Unlimited - 2001 and Beyond, B. Engquist, W. Schmid (eds), Springer, 2001
  2. O. Goldreich, A. Wigderson, Computational Complexity, in The Princeton Companion to Mathematics, T. Gowers (ed.), Princeton University Press, 2008
  3. C. O. Tuckey, The Construction for Mean Proportional, The Mathematical Gazette, Vol. 14, No. 203 (Oct., 1929), pp. 542-544
  4. D. E. Smith, Biography: Emile-Michel-Hyacinthe Lemoine, The American Mathematical Monthly, Vol. 3, No. 2 (Feb., 1896), pp. 29-33

Related material
Read more...

  • The Means
  • Averages, Arithmetic and Harmonic Means
  • Arithmetic and Geometric Means
  • Geometric Meaning of the Geometric Mean
  • Tangents, Perpendiculars and Geometric Mean

    • |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    71606854