Here's a problem: Construct a square with all four vertices on the sidelines of a given triangle ABC, so that two consecutive vertices lie on, say, AB.

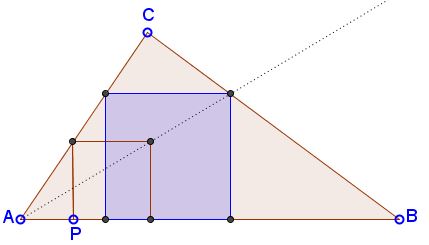
It's quite simple to construct a square with just three vertices on the sides of the triangle and the fourth vertex dangling free. For example, proceed as suggested by the applet. Start with a point P on AB. At P erect a perpendicular to AB till it cuts the side AC. Let d be the length of the perpendicular. Use it as the side length of the square. Note, that all such squares may be obtained from each other with central symmetry with center at A. This is also true of the unknown square that solves the problem. Hence the construction: draw a line through A and the dangling vertex till it intersects BC. From here drop a perpendicular to AB and draw a parallel to AB till it intersects AC. From here drop another perpendicular to AB.