Tangent to Circle in Three Steps
Problem
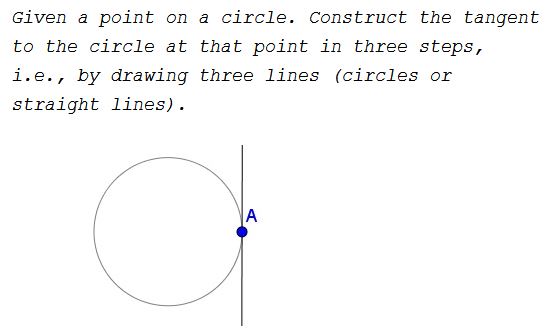
Hint
How many points does it take to define a line?
How many circles does it take to define a point?
Construction
Denote the given point $A.\,$
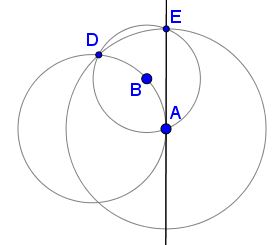
Choose an arbitrary point $B\,$ on the circle and draw circle $B(A),\,$ through $A\,$ centered at $B.\,$ Let $D\,$ be the other point of intersection of the two circles.
Draw the circle $A(D)\,$ through $D\,$ centered at $A.\,$ Mark point $E,\,$ the second intersection of $B(A)\,$ and $A(D).$
- Draw the line $AE.$
Proof 1 of the construction
Let $O\,$ be the center of the given circle.
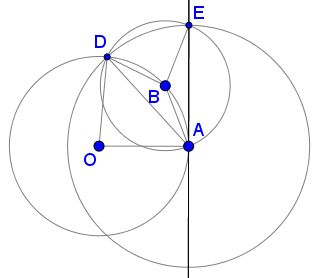
Assume $\angle AOD=2\alpha.\,$ Then $\angle OAD=90^{\circ}-\alpha\,$ and $\angle BAD=\displaystyle \frac{\alpha}{2},\,$ as inscribed angle subtended by half the arc $\overset{\frown}{AD}.$
By the construction, $\Delta ABD=\Delta ABE\,$ such that $\angle BAE=\angle BAD=\displaystyle \frac{\alpha}{2}.\,$ It follows that
$\displaystyle\begin{align}\angle OAE&=\angle OAD+\angle BAD+\angle BAE\\ &=(90^{\circ}-\alpha)+2\frac{\alpha}{2}=90^{\circ}. \end{align}$
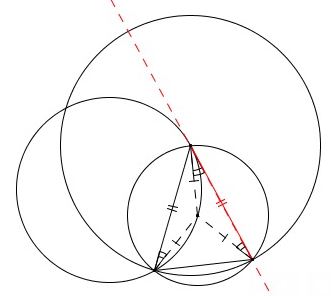
Proof 2 of the construction
The proof is simply an observation that the angle between the line and a chord equals the inscribed angle opposite the chord, and is therefore tangent.
Acknowledgment
The above problem comes from an uncommon site euclidea, devoted to the problems of Euclidean construction. The site and the problem have been brought to my attention by Konstantin Knop. Proof 2 is by Ted Courant.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73572601
