Short Runs from an Urn

Here is a problem by Neetu Badhoniya, K. S. Bhanu, and M. N. Deshpande (Institute of Science, Nagpur, India) from The American Mathematical Monthly (119, March 2012, pp 249-250) with the solution by Bob Tomper (Mathematics Department, University of North Dakota).

Solution

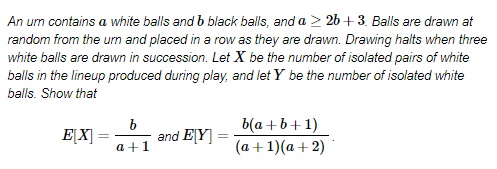
Short Runs from an Urn

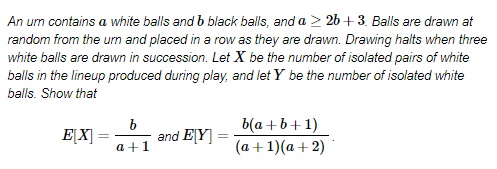
Solution

Solution is by Bob Tomper (Mathematics Department, University of North Dakota).

Let $E[X_{a,b}]$ and $E[Y_{a,b}]$ be the expected values of $X$ and $Y$ respectively when starting with an urn containing $a$ white balls and $b$ black balls, where $a \ge 2b + 3$.

For $a \ge 3$, we have $E[X_{a,0}]=E[Y_a,0]=0$, which agrees with the given formulae. We use induction on $b$, the number of black balls. Assume the formulae are correct up to $b - 1$, where $b \ge 1$ (and all appropriate $a$ values), and consider the case of $a$ white balls and $b$ black balls with $a \ge 2b + 3$.

The lineup begins with $B,$ $WB,$ $WWB,$ or $WWW,$ where $W$ and $B$ indicate drawing a white or a black ball, respectively. The last also ends the lineup; after each of the others, the number of white balls remaining in the urn is at least three more than twice the number of black balls, so the conditions for the induction hypothesis apply. Accounting for the isolated $W$ in $WB$ and the paired $WW$ in $WWB,$

$E[X_{a,b}]=P[B]\,E[X_{a,b-1}]+P[WB]\,E[X_{a-1,b-1}]+P[WWB]\,(1+E[X_{a-2,b-1}])$,

which gives an expression for $E[X_{a,b}]$:

$\displaystyle \frac{b}{a+b}\,\frac{b-1}{a+1}+\frac{a}{a+b}\,\frac{b}{a+b-1}\,\frac{b-1}{a}+\frac{a}{a+b}\,\frac{a-1}{a+b-1}\,\frac{b}{a+b-2}\left(1+\frac{b-1}{a-1}\right)$.

This simplifies to $\displaystyle \frac{b}{a+1}$. Similarly,

$E[Y_{a,b}]=P[B]\,E[Y_{a,b-1}]+P[WB]\,(1+E[Y_{a-1,b-1}])+P[WWB]\,(1+E[X_{a-2,b-1}])$,

and this simplifies to $\displaystyle \frac{b(a+b+1)}{(a+1)(a+2)}$.

71537101