Bear Born on a Tuesday

The answer to the question of how probable for two random bears to be both male, depends on additional information.

If, say, it is known that one of the bears is a male born on a Tuesday, what is the probability of the other bear to be also male?

The answer is rather surprising. Although a bear had to be born on one of the days of the week, the extra information of a specific day of birth affects the outcome of calculations.

Solution 1

Let's use the Principle of Proportionality which is just a shortcut for the employment of Bayes' Theorem.

The sample space for the gender of two bears is {ff, fm, mf, mm}, with f and m standing for "female: and "male", respectively. Denote these elementary events in sequence A₁, A₂, A₃, A₄. A priori probabilities for each of the possibilities are 1/4, 1/4, 1/4, 1/4; P(A_j) = 1/4, j = 1, 2, 3, 4.

Let B be the event of at one bear being a male born on a Tuesday. Consider the conditional probabilities: P(B|A₁) = 0, for in this case both bears are female. P(B|A₂) = P(B|A₃) = 1/7, because in the two cases the one male bear has the probability 1/7 to have been born on any specific day, Tuesday in particular. The most interesting case is A₄. The following table is suggestive:

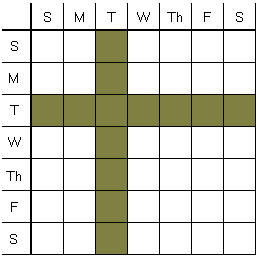
two bears birthdays

For two bears, there are 49 possible and equally probable birthday combinations; of these only 13 conform to the condition of at least "one bear being born on a Tuesday," making the probability P(B|A₄) = 13/49.

According to the Principle of Proportionality, the probabilities P(A₁|B), P(A₂|B), P(A₃|B), P(A₄|B) are proportional to 0, 1/7, 1/7, 13/49, respectively, and add up to 1. The coefficient of proportionality is then 1/7 + 1/7 + 13/49 = 27/49 which leads us to the conclusion that P(A₁|B) = 0, P(A₂|B) = P(A₃|B) = 1/7 ÷ 27/49 = 7/27, P(A₄|B) = 13/49 ÷ 27/49 = 13/27. We are, of course, only interested in the latter: the probability of both bears to be male, given that one of them is a male born on a Tuesday, is 13/27.

Solution 2

Let, as before, m stand for "male" and f for "female". Introduce also M to denote a male born on a Tuesday. to form the sample I shall differentiate the bears by their birthdays. Knowing that M is present, the sample space now consists of 7 Mf, 7 fM, and, based on the above diagram, 13 Mm pairs, counting the total of 27 elementary events. Of these, 13 count two male bears, giving the required probability 13/27, as above.

Remark

The problem originates with Gary Foshee who gave the shortest talk at the G4G9 (Gathering for Gardner 9) in 2010, just two months before M. Gardner passed away. The talk consisted of the three sentences "I have two children. One is a boy born on a Tuesday. What is the probability I have two boys?" The problem is certain to enter math folklore.

41162365