Chess Players Truel

Players A, B, and C play a series of chess games. Assume that A is the strongest player and C is the weakest one. Assume that there is no tie for each game. The winner of each game will play with the 3^rd player. The player who first gets 2 wins is the winner of the series. The player B determines who will play the 1^st game. Find the best choice for B. In general: if probability of A to win B is p > .5, probability B to win C is q > .5, probability A to win C is r, and r > p, evaluate chances of B.

Solution

|Contact| |Front page| |Contents| |Probability|

Copyright © 1996-2018 Alexander Bogomolny

Players A, B, and C play a series of chess games. Assume that A is the strongest player and C is the weakest one. Assume that there is no tie for each game. The winner of each game will play with the 3^rd player. The player who first gets 2 wins is the winner of the series. The player B determines who will play the 1^st game. Find the best choice for B. In general: if probability of A to win B is p > .5, probability B to win C is q > .5, probability A to win C is r, and r > p, evaluate chances of B.

The simplest way to approach the problem is by constructing an event tree. We are going to have three of them. The trees grow downwards starting with one of the pairs AB, BC or AC. Each node is a game, except for the terminal ones shown in double circles. These are the winners of the tournament who collected two wins first. For the first two trees we'll find the probability of B being the winner. These will be denoted P_AB and P_BC. We assume the outcomes of all games are independent.

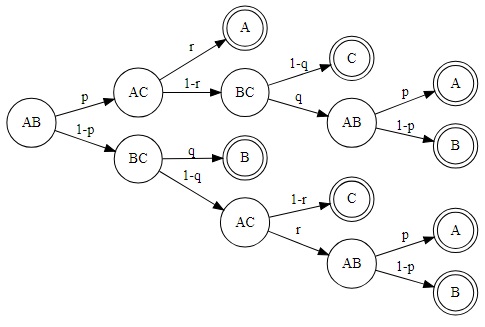
P_AB = p·(1 - r)·q·(1 - p) + (1 - p)·q + (1 - p)·(1 - q)·r·(1 - p).

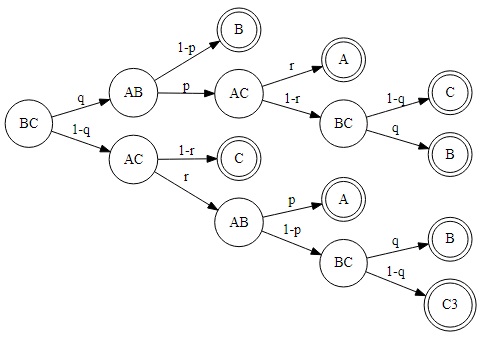
P_BC = q·(1 - p) + q·p·(1 - r)·q + (1 - q)·r·(1 - p)·q.

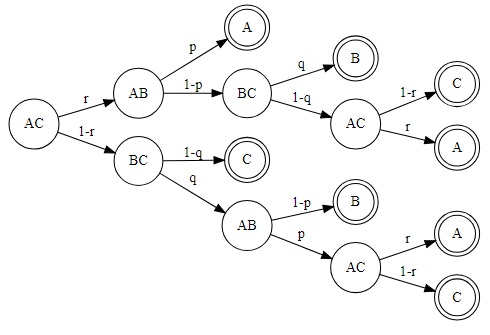
The task is to compare the two expressions P_AB and P_BC assuming p, q, r > .5 and r > p. You can play with the applet below to verify that always P_AB < P_BC which we shall prove below. The result is imminently plausible as it seems quite reasonable for B to start with playing the weakest player (C) first.

What if applet does not run?

So here are the two expressions to compare:

1. P_AB = p·(1 - r)·q·(1 - p) + (1 - p)·q + (1 - p)·(1 - q)·r·(1 - p).
2. P_BC = q·(1 - p) + q·p·(1 - r)·q + (1 - q)·r·(1 - p)·q.

In the difference P_BC - P_AB, the common term (1 - p)·q cancels out leading to

P_BC - P_AB= [p·q·(1 - r) + (1 - p)·(1 - q)·r]·(p + q - 1)

which, since p + q > .5 + .5 = 1, is positive. Note that this is true even without the condition r > p.

• What Is Probability?
• Intuitive Probability
• Probability Problems
• Sample Spaces and Random Variables
  • Importance of Having Sample Space Defined
• Probabilities
  • Example: A Poker Hand
  • Bernoulli Trials
  • Binomial Distribution
    • Getting Ahead by Two Points
  • Proofreading Example
  • Continuous Sample Spaces
    • Geometric Probability
    • Probability on Discrete Infinite Sets
    • Probability of Two Integers Being Comprime
• Conditional Probability
  • Bayes' Theorem
    • Bayesian Odds
    • Bayes' Ratio: Dramatic Taxicab Example
    • Principle of Proportionality
  • Conditional Recurrence
    • Laplace's Rule of Succession
• Dependent and Independent Events
  • Conditional Probability and Independent Events
  • Mutually (Jointly) Independent Events
  • Independent Events and Independent Experiments
• Algebra of Random Variables
• Expectation
  • Admittance to a Tennis Club
  • Average Number of Runs
  • Number of Trials to First Success
• Probability Generating Functions
  • Sicherman Dice
• Probability of Two Integers Being Coprime
• Random Walks
• Probabilistic Method
• Probability Paradoxes
  • Bertrand's Paradox
  • Monty Hall dilemma
  • Parrondo Paradox
• Symmetry Principle in Probability
  • d'Alembert's Misstep
  • Random Points on a Segment
  • Waiting for an Ace
• Non-transitive Dice

|Contact| |Front page| |Contents| |Probability|

Copyright © 1996-2018 Alexander Bogomolny