In a triangle, a median is a line joining a vertex with the mid-point of the opposite side. Using the standard notations, in ABC, there are three medians: AM_a, BM_b, CM_c. These three lines meet at a point - centroid of the triangle. Following are several proofs of this remarkable fact.

1. Elementary geometry
   

   A mid-line, i.e. the line joining the mid-points of two sides of a triangle, is parallel to the third side and equals its half (see, Euclid, Elements, VI.2 and VI.4.) Therefore, from ABC, M_bM_c = BC/2. Let G denote the point of intersection of BM_b and CM_c. Let also R be the mid-point of GC and S the mid-point of GB. Then as before, from GBC, RS = BC/2. Therefore RS = M_bM_c. Furthermore, the two lines are parallel (being both parallel to BC.) Thus, the quadrilateral M_bM_cSR is a parallelogram.

   Since diagonals of a parallelogram are halved by the point of intersection, we also have M_bG = GS and M_cG = GR which together with GS = SB and GR = RC show that, on both medians, G stands twice as far from one end (the vertex) than from the other end (the mid-point.) This condition uniquely defines a point on a median. Since for two medians the points thus defined coincide, the same, by symmetry, is true for the remaining median.

   

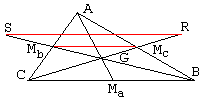
   Another elementary proof starts with extending BM_b beyond M_b to the length of GM_b. Similarly, CM_c extends beyond M_c to the length of GM_c. Then M_bM_c is the mid-line in both triangles ABC and GRS, whence SR = BC and the lines are parallel. This implies that the quadrilateral SRBC is a parallelogram, so that its diagonals CR and BS are halved by their common point G. Therefore, GM_b and GM_C are twice as short as respectively GB and GC. The proof ends as before.

   A third elementary proof was suggested by Scott Brodie. The triangles BCG and M_bM_cG are similar. All their sides are in the same proportion. Since BC/M_bM_c = 2, we also have BG/M_bG = 2 and CG/M_cG = 2.

   The fourth proof is due to Dani Rubinstein, Charles E. Smith Jewish Day School, Rockville, MD, which I came across in Mathematics Teacher, v 96, n 6, Sept. 2003, p. 401.

   

   Let G be the point of intersection of the medians AM_a and BM_b. Extend CG beyond G and further beyond its intersection with AB at D. Draw through B a line parallel to AM_a and let it intersect CG at H. In BCH, M_a is the midpoint of BC and also BH||GM_a. Therefore, G is the midpoint of CH. In ACH, M_b is the midpoint of AC, while G is the midpoint of CH. Therefore, AH||GM_b, or AH||BG. With two pairs of parallel sides, the quadrilateral AHBG is a parallelogram. In any parallelogram, the diagonals bisect each other. Hence, AD = DB. In other words, D = M_c, the midpoint of AB.

   As Dani points, his proof does not rely on the fact that the common point of the three medians divides each in the ratio 2:1, but rather obtains that ratio as a side effect.

2. Vector Algebra
   

   Consider two vectors a and b emanating from the same point O. Note that the same vector (a + b)/3 can be obtained in a couple of ways. First (the left diagram), find the average (a + b)/2 of the two vectors, and then multiply that vector by 2/3.

   On the other hand (the right diagram), the vector that connects the endpoint of a to the mid-point of b equals (b/2-a). Adding 2/3 of that vector to a, we get

   a + 2(b/2-a)/3 = a + b/3 - 2a/3 = (a + b)/3

   
   
3. Barycentric coordinates
   

   In the barycentric coordinates (w_A, w_B, w_C) with w_A + w_B + w_C =1, the equation of the median AM_a is w_B = w_C. Similarly, BM_b is defined by w_A = w_C and CM_c is defined by w_A = w_B. The four equations have a unique solution w_A = w_B = w_C = 1/3 which defines the common point of the three medians.

   With a reference to the transitivity of equality, the equations do not have to be solved explicitly. Transitivity immediately implies that the lines have a common point. Above we also found its barycentric coordinates.

4. Ceva Theorem
   

   The fact we are looking at is a corollary of a more general Ceva's Theorem.

5. Complex Numbers
   

   Points in the affine plane can be associated with complex numbers. For any two complex numbers z₁ and z₂, (z₁ + z₂)/2 is another complex number - the average of z₁ and z₂. There is a unique straight line that passes through two distinct complex numbers. Thus, if z₁ and z₂ are distinct, the equation of the line through the two points is z(t) = tz₁ + (1 - t)z₂, where t is an arbitrary real number.

   Let there be three complex numbers z_A, z_B, and z_C. Join the average of two points with the third point by a line: z(t) = tz_A + (1 - t)((z_B + z_C)/2. For t = 1/3 we get z(1/3) = (z_A + z_B + z_C)/3 - the average of the three numbers. The average of the three numbers lies on the line joining one of them with the average of the other two. Therefore, by symmetry, the average of the three belongs to all three such lines.

   A virtually identical argument works directly with points in the affine plane.

6. Affine Geometry
   

   In Affine Geometry, all triangles are the same in the sense that between any two triangles there exists an affine transformation that maps vertices of one triangle sequentially on the vertices of another. Affine transformations are known to preserve concurrency and its opposite, parallelism, of straight lines. It follows that if three medians intersect at one point in any one triangle, the same is true for all other triangles. (This can be put another way: affine transformations map the barycenters of a triangle to the barycenter of the image triangle, or barycenters are preserved under affine transformations.) Take the equilateral triangle as the reference triangle. In the equilateral triangle, all medians pass through the circumcenter. Which proves the statement in the general case. (Thanks to Scott Brodie for reminding me of this proof.) Any isosceles triangle could have served as a simple starting case. In an isosceles triangle, side medians meet on the axes of symmetry of the triangle which, among other things, serves as the third median.

   ---

   This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

   ---

   

   Here are a few related facts:

   1. The lines of the medians of triangles ABC and M_aM_bM_c coincide as, therefore, do their centroids. The latter also follows from the fact that the average of the three complex numbers (z_A + z_B)/2, (z_B + z_C)/2, and (z_A + z_C)/2 is exactly the same as the average of z_A, z_B, and z_B. This argument can be applied repetitively producing a sequence of nested triangles that all contain the same point G.

   2. Medians split a triangle into six smaller triangles of equal area. Cevians that possess this property are necessarily the medians. The centroid G is a unique point such that the triangles ABG, BCG, and ACG have the same area. Scott Brodie shares an interesting remark concerning the six triangles.

   3. If, in a triangle, two medians are equal then the triangle is isosceles. More generally, to a longer side there corresponds a shorter median.

   4. Among all points in the plane, centroid G minimizes the sum of squares to the vertices of the triangle ABC. To see that, first note that

      (1)	GA + GB + GC = 0,

      where I use the boldface to indicate vectors defined by their starting and ending points. (1) is another way of saying that G is the center of gravity of the three vertices A, B, C. (1) also follows from the observation that, since in the affine sense G = (A + B + C)/3, for any point X in the plane, we have

      (2)	(XA + XB + XC)/3 = XG,

      of which (1) is a particular case.

      Thus we are interested in minimizing f(X) = XA² + XB² + XC², where XA is the length of vector XA: XA = |XA|, i.e., the distance from X to A, and similarly XB and XC.

      XA2 + XB2 + XC2 = |XA|2 + |XB|2 + |XC|2   = |XG + GA|2 + |XG + GB|2 + |XG + GC|2   = |XG|2 + 2·XG·GA + |GA|2 + |XG|2 + 2·XG·GB + |GB|2 + |XG|2 + 2·XG·GC + |GC|2,

      where the dot denotes the scalar product. Let's continue:

      XA2 + XB2 + XC2 = 3·|XG|2 + 2·XG·(GA + GB + GC) + |GA|2 + |GB|2 + |GC|2   = 3·|XG|2 + |GA|2 + |GB|2 + |GC|2   |GA|2 + |GB|2 + |GC|2   = GA2 + GB2 + GC2,

      with the equality only when X = G.

   5. Medians in a triangle always form a triangle known as the median triangle of the given one. The area of the median triangle is 3/4 that of the given triangle (see a dynamic PWW and a more general setting.)

   6. Centroid of a triangle has an interesting characteristic property. Let a line through G intersect AB in M and AC in N. Then BM/MA + CN/NA = 1. Here, BM, MA, CN, NA are considered as signed segments. In a certain sense the identity even holds when the line in question is parallel to, say, AB. In this case, M is a point at infinity and BM/MA = -1 whereas CN/NA = 2. Conversely, if any line through a point P satisfies this identity, then necessarily P = G.

   

   

   Copyright © 1996-2008 Alexander Bogomolny