Three Similar Triangles
What is that about?
A Mathematical Droodle
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Explanation
This is what the applet purports to show:
Take any two similar triangles ABC and A'B'C' whose vertices are traversed in the same direction, either both clockwise or both counterclockwise. Divide AA', BB', CC' in equal proportions and connect the resulting points. The new triangle will be similar the the given two.
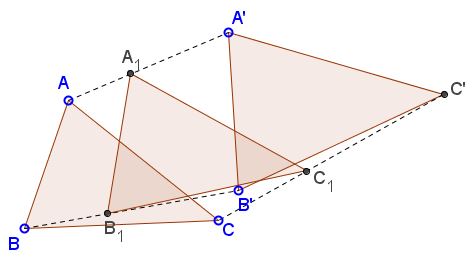
Think of the vertices as complex numbers. Two triangles ABC and A'B'C' are similar iff, say,
| (1) | 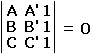 |
The assertion then follows from the well known properties of the determinants:
If a row or a column is multiplied by a constant factor, then the determinant is multiplied by the same factor.
A determinant does not change if a column (row) is added to another column (row.)
| (2) |  |
The first identity implies the second for any λ and μ, not both 0. In particular, (1) implies (2) for
We may also assert a partial converse. Assume (1) and
| (3) | 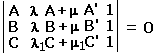 |
for some λ, μ, λ1, and μ1 with
Indeed, from (1) and (3) we derive
| (4) | (λ - λ1)C + (μ - μ1)C' = 0 |
and from the assumprions
| (5) | (λ - λ1) + (μ - μ1) = 0. |
If λ ≠ λ1, (4) and (5) imply C = C' contrary to our assumption.
The theorem just proved happens to be very useful for solving other problems:
References
- D. Wells, You Are a Mathematician, Dover, 1970
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73580983
