Two Circles and a Limit: What Is This About?
A Mathematical Droodle
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
A problem has been posted at the CTK Exchange and I also found it in a problem collection by E. J. Barbeau, M. S. Klamkin and W. O. J. Moser, and in another by J. Konhauser, D. Velleman, S. Wagon. It goes like this:
A stationary circle of radius $3$ is centered at $(3, 0).$ Another circle of variable radius $r$ is centered at the origin and meets the positive $y-axis$ in point $A.$ Let $B$ be the common point of the two circles in the upper half-plane. Let $E$ be the intersection of $AB,$ extended, with the $x-axis.$ What happens to $E$ as $r$ grows smaller and smaller?
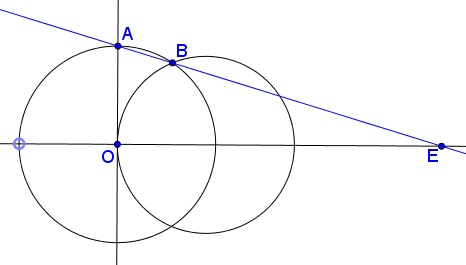
The curious fact about this problem is that, perhaps counterintuitively, $E$ does not recede to infinity as $r$ approaches $0.$ Instead, $E$ has a limit at point $(12, 0),$ or more generally, four times farther from the origin than the center of the stationary circle. Both at the CTK Exchange and in the both books the problem has been solved analytically and (in the first) also synthetically meaning that the value of the limit in question and its existence have been arrived at geometrically, rather than by deriving and investigating an algebraic formula. All geometric proofs shed light on the nature of the problem. Indeed, the last two proofs shine so brightly as to make the result altogether obvious.
References
- E. J. Barbeau, M. S. Klamkin, W. O. J. Moser, Five Hundred Mathematical Challenges, MAA, 1995, #396
- J. Konhauser, D. Velleman, S. Wagon, Which Way Did the Bicycle Go?, MAA, 1996, #5
Limits in Geometry
- Two Circles and a Limit
- A Geometric Limit
- Iterations in Geometry, an example
- Iterated Function Systems
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
73588732
