Cavalieri's Principle
Bonaventura Fransesco Cavalieri (1598-1647) was a disciple of Galileo. The most influential of his books, Geometria Indivisibilibus Continuorum Nova quadam ratione promota, has ben completed in 1629 and published in 1635. The following excerpt, known as Cavalieri's theorem or Cavalieri's principle, is taken from Book VII, Theorem 1, Proposition 1.
The Theorem. If between the same parallels any two plane figures are constructed, and if in them, any straight lines being drawn equidistant from the parallels, the included portions of any one of these lines are equal, the plane figures are also equal to one another; and if between the same parallel planes any solid figures are constructed, and if in them, any planes being drawn equidistant from the parallel planes, the included plane figures out of any one of the planes so drawn are equal, the solid figures are likewise equal to one another.
The applet below provides an illustration to the theorem which is rather trivial in case the shapes between the parallels are all rectangles, even if different dimensions. The applet shows two sets of rectangles. In one, the rectangles can be dragged as a whole. In the other, the short sides of the rectangles can be dragged to modify their dimension. However, they are modified, the two shapes formed by the rectangles always maintain equal areas.
| What if applet does not run? |
Cavalieri's principle reveals its power when applied to more complicated shapes (or when the rectangles are allowed to become infinitely thin.) A short formulation requires two solids (plane figures) to have the same height and the same areas (lengths) on every level, stipulating that such shapes have equal volumes (areas). The principle was an early advance towards what is now known as the Integral Calculus.
As a remarkable application of Cavalieri's principle, let's find a connection between the volumes of a cylinder, a cone and a sphere.
(The diagram below has been released into the public domain via wikipedia.org.)
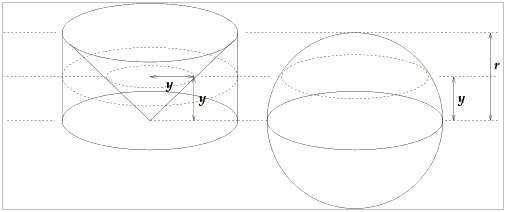
Assume the height of a cylinder equals the radius of its base r and that a cone with the same base and height is inscribed in the cylinder, as shown.
Measuring from the bottom, the area of the cross-section of the cone at level y equals π y². The cross-section of the cylinder, independent of its height, equals π r², meaning that the area of the remaining ring (at level y) equals
The volume of a cylinder is Base×Height, the volume of the cone is 1/3 of that. Therefore the volume of the hemisphere is 2/3 of the cylinder and that of the whole sphere is 4/3 of the volume of the cylinder. The latter is π r³, making the volume of the sphere
References
- D. E. Smith, A Source Book in Mathematics, Dover, 1959
- D. J. Struik, A Source Book in Mathematics 1200-1800, Princeton University Press, 1990 (Third printing)
|Activities| |Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
73583477
